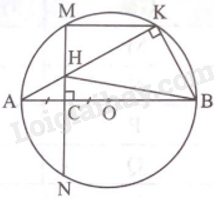
Giải bài 5 trang 82 sách bài tập toán 9 - Chân trời sáng tạo tập 2Cho đường tròn (O), đường kính AB, C là trung điểm của OA và dây MN vuông góc với OA tại C. Gọi K là điểm tuỳ ý trên cung nhỏ BM, H là giao điểm của AK và MN. Chứng minh BCHK là tứ giác nội tiếp. Đề bài Cho đường tròn (O), đường kính AB, C là trung điểm của OA và dây MN vuông góc với OA tại C. Gọi K là điểm tuỳ ý trên cung nhỏ BM, H là giao điểm của AK và MN. Chứng minh BCHK là tứ giác nội tiếp. Phương pháp giải - Xem chi tiết Chứng minh tam giác BCH vuông tại C và tam giác BKH vuông tại K cùng nội tiếp đường tròn đường kính HB suy ra BCHK nội tiếp đường tròn đường kính HB. Lời giải chi tiết
Ta có \(\widehat {AKB} = {90^o}\) (góc nội tiếp chắn nửa đường tròn) hay \(\widehat {HKB} = {90^o}\). Tam giác BCH vuông tại C (\(\widehat {HCB} = {90^o}\)(gt)) và tam giác BKH vuông tại K cùng nội tiếp đường tròn đường kính HB. Do đó, tứ giác BCHK nội tiếp đường tròn đường kính HB.
|