Giải bài 5.4 trang 56 sách bài tập toán 9 - Kết nối tri thức tập 1Trên mặt phẳng tọa độ Oxy, cho điểm A(3; 1). Gọi B, C và D là các điểm đối xứng với A lần lượt qua trục hoành, qua gốc O và qua trục tung. a) Xác định tọa độ của ba điểm B, C và D. b) Có hay không một đường tròn đi qua bốn điểm A, B, C và D. Xác định tâm và bán kính của đường tròn đó, nếu có. Đề bài Trên mặt phẳng tọa độ Oxy, cho điểm A(3; 1). Gọi B, C và D là các điểm đối xứng với A lần lượt qua trục hoành, qua gốc O và qua trục tung. a) Xác định tọa độ của ba điểm B, C và D. b) Có hay không một đường tròn đi qua bốn điểm A, B, C và D. Xác định tâm và bán kính của đường tròn đó, nếu có. Phương pháp giải - Xem chi tiết a) - Vì B đối xứng với A qua trục hoành nên: + AB vuông góc với Ox, suy ra A và B có cùng hoành độ. + A và B cách đều Ox, nên A và B có tung độ đối nhau. - Vì C đối xứng với A qua gốc O nên O là trung điểm của AC. Do đó, A và C có hoành độ và tung độ đối nhau. - Vì D đối xứng với A qua trục tung nên: + AD vuông góc với Oy, suy ra A và D có cùng tung độ. + A và D cách đều Oy, nên A và D có hoành độ đối nhau. b) + Gọi H là hình chiếu của D trên trục Ox. Khi đó, H(-3; 0) và DH vuông góc với OH. + Áp dụng định lí Pythagore vào tam giác DOH vuông tại H tính được \(OD = \sqrt {10} \) + Tương tự ta tính được \(OA = OB = OC = \sqrt {10} \) + Vì \(OA = OB = OC = OD = \sqrt {10} \) nên bốn điểm A, B, C và D cùng thuộc đường tròn (O, \(\sqrt {10} \)). Lời giải chi tiết
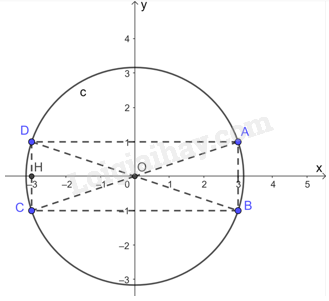
a) Vì B đối xứng với A qua trục hoành nên: + AB vuông góc với Ox, suy ra A và B có cùng hoành độ. + A và B cách đều Ox, nên A và B có tung độ đối nhau. Suy ra: B(3; -1) Vì C đối xứng với A qua gốc O nên O là trung điểm của AC. Do đó, A và C có hoành độ và tung độ đối nhau. Suy ra C(-3; -1). Vì D đối xứng với A qua trục tung nên: + AD vuông góc với Oy, suy ra A và D có cùng tung độ. + A và D cách đều Oy, nên A và D có hoành độ đối nhau. Suy ra D(-3; 1). b) Gọi H là hình chiếu của D trên trục Ox. Khi đó, H(-3; 0) và DH vuông góc với OH. Áp dụng định lí Pythagore vào tam giác DOH vuông tại H ta có: \(O{D^2} = D{H^2} + O{H^2} = {1^2} + {3^2} = 10\) nên \(OD = \sqrt {10} \). Tương tự ta có: \(OA = OB = OC = \sqrt {10} \). Vì \(OA = OB = OC = OD = \sqrt {10} \) nên bốn điểm A, B, C và D cùng thuộc đường tròn (O, \(\sqrt {10} \)).
|