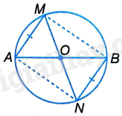
Giải bài 5.5 trang 56 sách bài tập toán 9 - Kết nối tri thức tập 1Cho đường tròn (O), đường kính AB và điểm M thuộc (O) (M không trùng với điểm nào trong hai điểm A và B). Trên (O) lấy điểm N nằm khác phía của M đối với đường thẳng AB sao cho (AM = BN). Chứng minh rằng O là trung điểm của đoạn MN. GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho HocTot.XYZ và nhận về những phần quà hấp dẫn Đề bài Cho đường tròn (O), đường kính AB và điểm M thuộc (O) (M không trùng với điểm nào trong hai điểm A và B). Trên (O) lấy điểm N nằm khác phía của M đối với đường thẳng AB sao cho AM=BN. Chứng minh rằng O là trung điểm của đoạn MN. Phương pháp giải - Xem chi tiết + Chứng minh ΔAOM=ΔBON(c.c.c), suy ra ^MAO=^NBO, từ đó chứng minh được AM//BN. + Chứng minh tứ giác AMBN là hình bình hành, suy ra O là trung điểm của đoạn MN. Lời giải chi tiết
Tam giác AOM và tam giác BON có: OA=OB,OM=ON,AM=BN nên ΔAOM=ΔBON(c.c.c). Suy ra ^MAO=^NBO, mà hai góc này ở vị trí so le trong nên AM//BN. Tứ giác AMBN có: AM//BN, AM=BN nên AMBN là hình bình hành. Mà O là trung điểm của AB nên O là trung điểm của đoạn MN.  Chia sẻ Bình luận
Tham Gia Group Dành Cho Lớp 9 - Ôn Thi Vào Lớp 10 Miễn Phí
|
