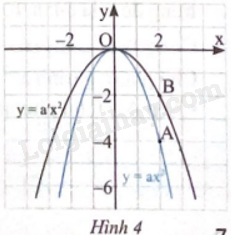
Giải bài 6 trang 7 sách bài tập toán 9 - Chân trời sáng tạo tập 2Cho đồ thị của các hàm số y = ax2 (a( ne )0) và y = a’x2 (a’( ne )0) (Hình 4). Cho biết điểm A thuộc đồ thị của hàm số y = ax2, điểm B thuộc đồ thị của hàm số y = a’x2. a) Xác định các hệ số a và a’ b) Lấy điểm A’ đối xứng với A qua trục tung. Điểm A’ có thuộc đồ thị hàm số y = ax2 không? Vì sao? c) Biết rằng điểm M(4; b) thuộc đồ thị của hàm số y = a’x2, hãy tính b. Điểm M’ (- 4; b) có thuộc đồ thị của hàm số y = a’x2 không? Vì sao? Đề bài Cho đồ thị của các hàm số y = ax2 (a \( \ne \) 0) và y = a’x2 (a’ \( \ne \) 0) (Hình 4).
Cho biết điểm A thuộc đồ thị của hàm số y = ax2, điểm B thuộc đồ thị của hàm số y = a’x2. a) Xác định các hệ số a và a’ b) Lấy điểm A’ đối xứng với A qua trục tung. Điểm A’ có thuộc đồ thị hàm số y = ax2 không? Vì sao? c) Biết rằng điểm M(4; b) thuộc đồ thị của hàm số y = a’x2, hãy tính b. Điểm M’ (- 4; b) có thuộc đồ thị của hàm số y = a’x2 không? Vì sao? Phương pháp giải - Xem chi tiết Nhìn đồ thị xác định điểm A, B thay lần lượt vào y = ax2 và y = a’x2 để tìm a và a’.. Xác định điểm A’, M’ rồi kiểm tra có thuộc y = ax2 và y = a’x2 rồi kết luận. Lời giải chi tiết a) Thay toạ độ điểm A(2; - 4) vào y = ax2 , ta tìm được a = - 1. Vậy (P): y = - x2. Thay toạ độ điểm B(2; -2) vào y = a’x2 , ta tìm được a’ = \( - \frac{1}{2}\). Vậy (P): y = \( - \frac{1}{2}\)x2. b) Điểm A’ đối xứng với điểm A qua trục tung nên A’(- 2; 4). Do đó điểm A’(- 2; - 4) cũng thuộc (P). c) Thay toạ độ điểm M(4; b) vào y = \( - \frac{1}{2}\)x2 , ta tìm được b = -8. Suy ra M(4; - 8). Điểm M’(-4; -8) đối xứng với điểm M qua trục tung, do đó M’ thuộc (P’).
|