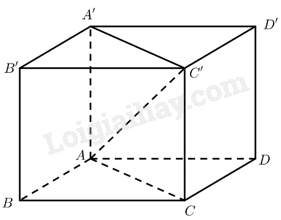
SBT Toán 12 - giải SBT Toán 12 - Chân trời sáng tạo

Giải bài 8 trang 64 sách bài tập toán 12 - Chân trời sáng tạo

Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ . Gọi $x,y,z$ theo thứ tự là số đo các góc hợp bởi vectơ $\overrightarrow {AC'}$ với các vectơ $\overrightarrow {AB} ,\overrightarrow {AD} ,\overrightarrow {AA'}$ . Chứng minh ${\cos ^2}x + {\cos ^2}y + {\cos ^2}z = 1$ .

Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Hoá - Sinh - Sử - Địa

Đề bài

Chứng minh ${\cos ^2}x + {\cos ^2}y + {\cos ^2}z = 1$ .

Phương pháp giải - Xem chi tiết

Sử dụng định lý Pitago.

Lời giải chi tiết

Gọi $a,b,c,d$ lần lượt là độ dài của $AB,A{\rm{D}},AA',AC'$ .

Tam giác $ABC$ vuông tại $B \Rightarrow A{C^2} = A{B^2} + B{C^2}$ .

Tam giác $ACC'$ vuông tại $C$

$\Rightarrow AC{'^2} = A{C^2} + CC{'^2} = A{B^2} + B{C^2} + AA{'^2}$

Do đó ${d^2} = {a^2} + {b^2} + {c^2}$ .

Ta có: $\cos x = \frac{{AB}}{{AC'}} = \frac{a}{d},\cos y = \frac{{AD}}{{AC'}} = \frac{b}{d},\cos z = \frac{{AA'}}{{AC'}} = \frac{c}{d}$

${\cos ^2}x + {\cos ^2}y + {\cos ^2}z = {\left( {\frac{a}{d}} \right)^2} + {\left( {\frac{b}{d}} \right)^2} + {\left( {\frac{c}{d}} \right)^2} = \frac{{{a^2}}}{{{d^2}}} + \frac{{{b^2}}}{{{d^2}}} + \frac{{{c^2}}}{{{d^2}}} = \frac{{{a^2} + {b^2} + {c^2}}}{{{d^2}}} = \frac{{{d^2}}}{{{d^2}}} = 1$ .

Chia sẻ

Bình luận

Bình chọn:

4.9 trên 7 phiếu

Giải bài 9 trang 64 sách bài tập toán 12 - Chân trời sáng tạo
Tính độ lớn của các lực căng trên mỗi sợi dây cáp trong Hình 16. Cho biết khối lượng xe là 1900 kg, gia tốc là 10 m/s, khung nâng có khối lượng 100 kg và có dạng hình chóp $S.ABCD$ với đáy $ABCD$ là hình chữ nhật tâm $O$ , $AB=8m,BC=12m,SC=12m$ và $SO$ vuông góc với $\left( {ABCD} \right)$ . Làm tròn kết quả đến hàng đơn vị của Newton.
Giải bài 7 trang 64 sách bài tập toán 12 - Chân trời sáng tạo
Một tàu kéo một xà lan trên biển di chuyển được 3 km với một lực kéo có cường độ 2000 N và có phương hợp với phương dịch chuyển một góc ({30^ circ }). Tính công thực hiện bởi lực kéo nói trên (kết quả làm tròn đến hàng đơn vị của Jun).
Giải bài 6 trang 63 sách bài tập toán 12 - Chân trời sáng tạo
Cho hình hộp (ABCD.A'B'C'D') có tất cả các cạnh bằng (a) và cho biết (widehat {BAD} = widehat {BAA'} = widehat {DAA'} = {60^ circ }). Tính các tích vô hướng sau: a) (overrightarrow {AB} .overrightarrow {AD} ); b) (overrightarrow {DA} .overrightarrow {DC} ); c) (overrightarrow {AA'} .overrightarrow {AC} ).
Giải bài 5 trang 63 sách bài tập toán 12 - Chân trời sáng tạo
Cho hình lập phương $ABCD.A'B'C'D'$ . Gọi $O,O'$ lần lượt là tâm của các hình vuông $ABCD$ và $A'B'C'D'$ ; $I$ là giao điểm của $AC'$ và $A'C$ . Chứng minh rằng: a) $\overrightarrow {OA'} + \overrightarrow {OB'} + \overrightarrow {OC'} + \overrightarrow {OD'} = 4\overrightarrow {OO'}$ ; b) $\overrightarrow {DB} + \overrightarrow {DD'} = 2\overrightarrow {DI}$ .
Giải bài 4 trang 63 sách bài tập toán 12 - Chân trời sáng tạo
Cho hình hộp $ABCD.A'B'C'D'$ có $AC'$ và $A'C$ cắt nhau tại $O$ . Cho biết $AO = a$ . Tính theo $a$ độ dài các vectơ: a) $\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'}$ ; b) $\overrightarrow {C'B'} + \overrightarrow {C'D'} + \overrightarrow {A'A}$ .

Luyện Bài Tập Trắc nghiệm Toán 12 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.