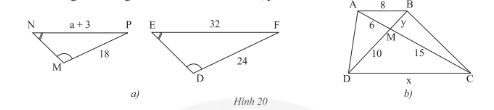
Giải bài 8 trang 72 SGK Toán 8 tập 2– Chân trời sáng tạo

Đề bài

a) Trong Hình 20a, cho biết $\widehat N = \widehat E,\widehat M = \widehat D,MP = 18m,DF = 24m,$$EF = 32m,$$NP = a + 3\left( m \right)$. Tìm $a$.

b) Cho $ABCD$ là hình thang $\left( {AB//CD} \right)$ (Hình 20b).

Chứng minh rằng $\Delta AMB\backsim\Delta CMD$. Tìm $x,y$.

 

Lời giải chi tiết

a) Xét tam giác $MNP$ tam giác $DEF$ ta có:

$\widehat M = \widehat D$ (giả thuyết)

$\widehat N = \widehat E$ (giả thuyết)

Do đó, $\Delta MNP\backsim\Delta DEF$ (g.g)

Suy ra, $\frac{{MP}}{{DF}} = \frac{{NP}}{{EF}} \Rightarrow \frac{{18}}{{24}} = \frac{{a + 3}}{{32}} \Rightarrow a + 3 = \frac{{18.32}}{{24}} = 24 \Leftrightarrow a = 24 - 3 = 21$.

Vậy $a = 21m$.

b) Vì $ABCD$ là hình thang nên $AB//CD$.

Vì $AB//CD \Rightarrow \widehat {ABM} = \widehat {MDC}$ (hai góc so le trong) và $AB//CD \Rightarrow \widehat {BAM} = \widehat {MCD}$ (hai góc so le trong)

Xét tam giác $AMB$ và tam giác $CMD$ có:

$\widehat {ABM} = \widehat {MDC}$ (chứng minh trên)

$\widehat {BAM} = \widehat {MCD}$ (chứng minh trên)

Do đó, $\Delta AMB\backsim\Delta CMD$ (g.g).

Ta có:

$\frac{{AM}}{{CM}} = \frac{{BM}}{{DM}} = \frac{{AB}}{{CD}} \Leftrightarrow \frac{6}{{15}} = \frac{y}{{10}} = \frac{8}{x}$.

Ta có: $\frac{6}{{15}} = \frac{y}{{10}} \Rightarrow y = \frac{{10.6}}{{15}} = 4$

$\frac{6}{{15}} = \frac{8}{x} \Rightarrow x = \frac{{8.15}}{6} = 20$.

Vậy $x = 20;y = 4$.