Giải câu hỏi mục 1 trang 89, 91 SGK Toán 12 tập 1 - Cánh diều

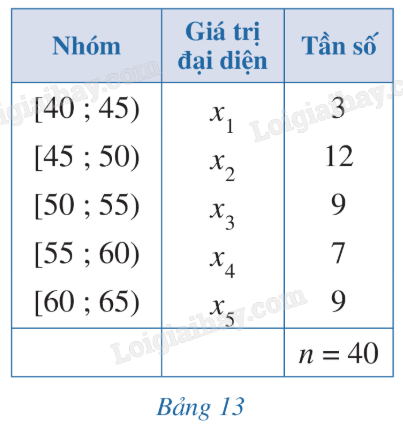
HĐ

Trả lời câu hỏi Hoạt động trang 89 SGK Toán 12 Cánh diều

Xét mẫu số liệu ghép nhóm cho bởi bảng 13.

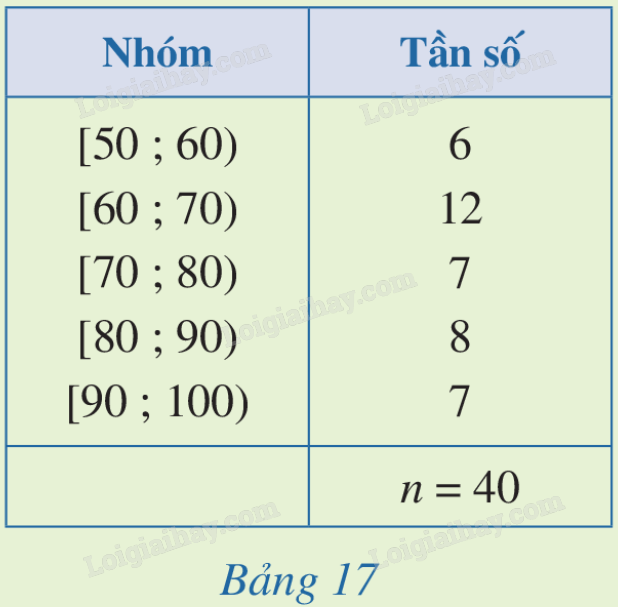
a) Tìm \({x_1},{x_2},{x_3},{x_4},{x_5}\) lần lượt là giá trị đại diện của nhóm 1, nhóm 2, nhóm 3, nhóm 4, nhóm 5.

b) Tính số trung bình cộng \(\overline x \) của mẫu số liệu ghép nhóm đó.

c) Tính \({s^2} = \frac{{3.{{({x_1} - \overline x )}^2} + 12{{({x_2} - \overline x )}^2} + 9{{({x_3} - \overline x )}^2} + 7{{({x_4} - \overline x )}^2} + 9{{({x_5} - \overline x )}^2}}}{{40}}\).

d) Tính \(s = \sqrt {{s^2}} \).

Phương pháp giải:

Quan sát bảng số liệu và áp dụng công thức.

Lời giải chi tiết:

a) \({x_1} = 42,5;{x_2} = 47,5;{x_3} = 52,5;{x_4} = 57,5;{x_5} = 62,5\).

b) \(\overline x  = \frac{{3.42,5 + 12.47,5 + 9.52,5 + 7.57,5 + 9.62,5}}{{40}} = 53,375\).

c) \({s^2} = \frac{{3.{{({x_1} - \overline x )}^2} + 12{{({x_2} - \overline x )}^2} + 9{{({x_3} - \overline x )}^2} + 7{{({x_4} - \overline x )}^2} + 9{{({x_5} - \overline x )}^2}}}{{40}}\)

\( = \frac{{3.{{(42,5 - 53,375)}^2} + 12{{(47,5 - 53,375)}^2} + 9{{(52,5 - 53,375)}^2} + 7{{(57,5 - 53,375)}^2} + 9{{(62,5 - 53,375)}^2}}}{{40}}\)

\( = \frac{{2631}}{{64}}\).

d) \(s = \sqrt {{s^2}}  = \sqrt {\frac{{2631}}{{64}}}  \approx 6,41\).

LT

Trả lời câu hỏi Luyện tập trang 91 SGK Toán 12 Cánh diều

Tính phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm cho ở Bảng 17 (làm tròn kết quả đến hàng phần mười).

Phương pháp giải:

Áp dụng công thức tính phương sai, độ lệch chuẩn.

Lời giải chi tiết:

Số trung bình của mẫu số liệu là:

\(\overline x  = \frac{{6.55 + 12.65 + 7.75 + 8.85 + 7.95}}{{40}} = \frac{{2980}}{{40}} = 74,5\).

Phương sai của mẫu số liệu là:

\({s^2} = \frac{1}{{40}}.[6.{(55 - 74,5)^2} + 12.{(65 - 74,5)^2} + 7.{(75 - 74,5)^2}\)

\( + 8.{(85 - 74,5)^2} + 7.{(95 - 74,5)^2}] = \frac{{7190}}{{40}} \approx 179,8\).

Độ lệch chuẩn của mẫu số liệu là:

\(\sqrt {{s^2}}  = \sqrt {\frac{{7190}}{{40}}}  \approx 13,4\).