Giải mục 1 trang 15,16,17 SGK Toán 12 tập 1 - Kết nối tri thứcĐịnh nghĩa
Lựa chọn câu để xem lời giải nhanh hơn
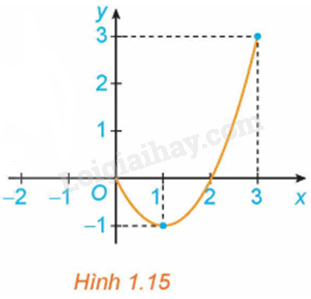
HĐ1 Trả lời câu hỏi Hoạt động 1 trang 15 SGK Toán 12 Kết nối tri thức Cho hàm số \(y = f\left( x \right) = {x^2} - 2x\) với \(x \in \left[ {0;3} \right]\), có đồ thị như Hình 1.15.
a) Giá trị lớn nhất M của hàm số trên đoạn \(\left[ {0;3} \right]\) là bao nhiêu? Tìm \({x_0}\) sao cho \(f\left( {{x_0}} \right) = M\). b) Giá trị nhỏ nhất m của hàm số trên đoạn \(\left[ {0;3} \right]\) là bao nhiêu? Tìm \({x_0}\) sao cho \(f\left( {{x_0}} \right) = m\). Phương pháp giải: Sử dụng kiến thức về đọc hiểu đồ thị hàm số. Lời giải chi tiết: a) Giá trị lớn nhất của đồ thị hàm số trên đoạn \(\left[ {0;3} \right]\) là \(M = 3\). Với \({x_0} = 3\) thì \(f\left( 3 \right) = 3\). b) Giá trị nhỏ nhất của đồ thị hàm số trên đoạn \(\left[ {0;3} \right]\) là \(m = - 1\). Với \({x_0} = 1\) thì \(f\left( 1 \right) = - 1\). LT1 Trả lời câu hỏi Luyện tập 1 trang 17 SGK Toán 12 Kết nối tri thức Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: a) \(y = \sqrt {2x - {x^2}} \); b) \(y = - x + \frac{1}{{x - 1}}\) trên khoảng \(\left( {1; + \infty } \right)\). Phương pháp giải: Sử dụng kiến thức về khái niệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số để tính: Cho hàm số \(y = f\left( x \right)\) xác định trên tập D. + Số M được gọi là giá trị lớn nhất của hàm số \(y = f\left( x \right)\) trên tập D nếu \(f\left( x \right) \le M\) với mọi \(x \in D\) và tồn tại \({x_0} \in D\) sao cho \(f\left( {{x_0}} \right) = M\). Kí hiệu \(M = \mathop {\max }\limits_{x \in D} f\left( x \right)\) hoặc \(M = \mathop {\max }\limits_D f\left( x \right)\) + Số m được gọi là giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên tập D nếu \(f\left( x \right) \ge m\) với mọi \(x \in D\) và tồn tại \({x_0} \in D\) sao cho \(f\left( {{x_0}} \right) = m\). Kí hiệu \(m = \mathop {\min }\limits_{x \in D} f\left( x \right)\) hoặc \(m = \mathop {\min }\limits_D f\left( x \right)\) Lời giải chi tiết: a) Tập xác định của hàm số là \(\left[ {0;2} \right]\). Với \(x \in \left[ {0;2} \right]\) ta có: \(y' = \frac{{\left( {2x - {x^2}} \right)'}}{{2\sqrt {2x - {x^2}} }} = \frac{{ - x + 1}}{{\sqrt {2x - {x^2}} }}\), \(y' = 0 \Leftrightarrow \frac{{ - x + 1}}{{\sqrt {2x - {x^2}} }} = 0 \Leftrightarrow x = 1\left( {tm} \right)\) Lập bảng biến thiên của hàm số trên đoạn \(\left[ {0;2} \right]\):
Từ bảng biến thiên ta thấy: \(\mathop {\min }\limits_{\left[ { - 1;1} \right]} f\left( x \right) = f\left( 0 \right) = f\left( 2 \right) = 0,\mathop {\max }\limits_{\left[ { - 1;1} \right]} f\left( x \right) = f\left( 1 \right) = 1\). b) Với \(x \in \left( {1; + \infty } \right)\) ta có: Ta có: \(y' = - 1 + \frac{{ - 1}}{{{{\left( {x - 1} \right)}^2}}} < 0\;\forall x \in \left( {1; + \infty } \right)\) \(\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \left( { - x + \frac{1}{{x - 1}}} \right) = + \infty ;\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( { - x + \frac{1}{{x - 1}}} \right) = - \infty \) Lập bảng biến thiên của hàm số trên \(\left( {1; + \infty } \right)\):
Vậy hàm số không có giá trị lớn nhất, giá trị nhỏ nhất trên \(\left( {1; + \infty } \right)\).
|