Giải mục 1 trang 50, 51, 52 SGK Toán 12 tập 2 - Cánh diềuVecto pháp tuyến. Cặp vecto chỉ phương của mặt phẳng
Lựa chọn câu để xem lời giải nhanh hơn
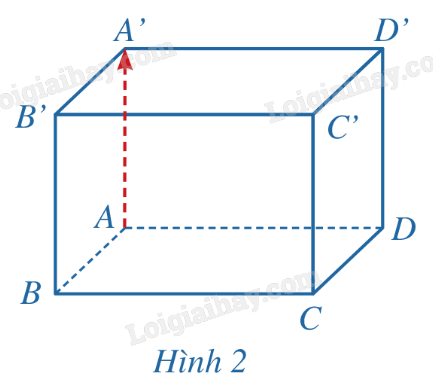
HĐ1 Trả lời câu hỏi Hoạt động 1 trang 50 SGK Toán 12 Cánh diều Cho hình hộp chữ nhật ABCD.A’B’C’D’ (Hình 2). Giá của vecto \(\overrightarrow {AA'} \) có vuông góc với mặt phẳng (ABCD) hay không?
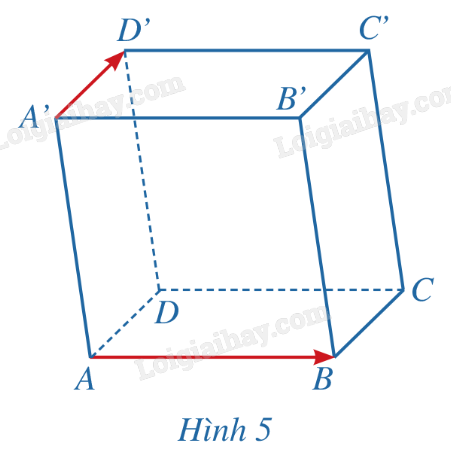
Phương pháp giải: Quan sát hình vẽ. Lời giải chi tiết: Vì AA' vuông góc với mặt phẳng (ABCD) nên giá của vecto \(\overrightarrow {AA'} \) cũng vuông góc với mặt phẳng (ABCD). LT1 Trả lời câu hỏi Luyện tập 1 trang 51 SGK Toán 12 Cánh diều Trong không gian với hệ tọa độ Oxyz, hãy chỉ ra một vecto pháp tuyến của: a) Mặt phẳng (Oyz); b) Mặt phẳng (Ozx). Phương pháp giải: Tìm vecto có giá vuông góc với mặt phẳng. Lời giải chi tiết: a) Vecto \(\overrightarrow i = (1;0;0)\) có giá là trục Ox và \(Ox \bot (Oyz)\) nên \(\overrightarrow i = (1;0;0)\) là một vecto pháp tuyến của mặt phẳng (Oyz). b) Vecto \(\overrightarrow j = (0;1;0)\) có giá là trục Oy và \(Oy \bot (Ozx)\) nên \(\overrightarrow j = (0;1;0)\) là một vecto pháp tuyến của mặt phẳng (Ozx). HĐ2 Trả lời câu hỏi Hoạt động 2 trang 51 SGK Toán 12 Cánh diều Cho hình hộp ABCD.A’B’C’D’. Cho biết hai vecto \(\overrightarrow {AB} \), \(\overrightarrow {A'D'} \) có cùng phương hay không. Nhận xét về vị trí tương đối giữa giá của mỗi vecto \(\overrightarrow {AB} \), \(\overrightarrow {A'D'} \) và mặt phẳng (ABCD) (Hình 5)
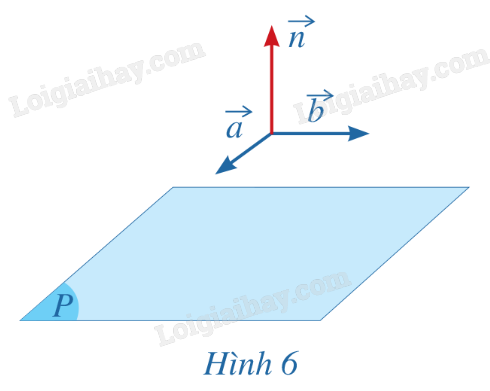
Phương pháp giải: Quan sát hình vẽ. Lời giải chi tiết: Hai vecto \(\overrightarrow {AB} \), \(\overrightarrow {A'D'} \) không cùng phương. Giá của vecto \(\overrightarrow {AB} \) nằm trong mặt phẳng (ABCD). Giá của vecto \(\overrightarrow {A'D'} \) song song với mặt phẳng (ABCD). LT2 Trả lời câu hỏi Luyện tập 2 trang 51 SGK Toán 12 Cánh diều Trong không gian với hệ tọa độ Oxyz, hãy chỉ ra một cặp vecto chỉ phương của mỗi mặt phẳng (Oxy), (Oyz), (Ozx). Phương pháp giải: Tìm cặp vecto không cùng phương, có giá song song hoặc thuộc mặt phẳng. Lời giải chi tiết: Do hai vecto \(\overrightarrow i \), \(\overrightarrow j \) không cùng phương và có giá cùng nằm trong mặt phẳng (Oxy) nên \(\overrightarrow i \), \(\overrightarrow j \) là cặp vecto chỉ phương của mặt phẳng (Oxy). Do hai vecto \(\overrightarrow j \), \(\overrightarrow k \) không cùng phương và có giá cùng nằm trong mặt phẳng (Oyz) nên \(\overrightarrow j \), \(\overrightarrow k \) là cặp vecto chỉ phương của mặt phẳng (Oyz). Do hai vecto \(\overrightarrow k \), \(\overrightarrow i \) không cùng phương và có giá cùng nằm trong mặt phẳng (Oyz) nên \(\overrightarrow k \), \(\overrightarrow i \) là cặp vecto chỉ phương của mặt phẳng (Ozx). HĐ3 Trả lời câu hỏi Hoạt động 3 trang 52 SGK Toán 12 Cánh diều Cho cặp vecto chỉ phương \(\overrightarrow a = (1;0;1)\), \(\overrightarrow b = (2;1;0)\) của mặt phẳng (P).
a) Hãy chỉ ra tọa độ của một vecto \(\overrightarrow n (\overrightarrow n \ne \overrightarrow 0 )\) vuông góc với cả hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) (Hình 6). b) Vecto \(\overrightarrow n \) có là vecto pháp tuyến của mặt phẳng (P) hay không? Phương pháp giải: a) Cho hai vecto \(\overrightarrow u = ({x_1};{y_1};{z_1})\) và \(\overrightarrow v = ({x_2};{y_2};{z_2})\) không cùng phương. Khi đó, vecto \(\overrightarrow w = ({y_1}{z_2} - {y_2}{z_1};{z_1}{x_2} - {z_2}{x_1};{x_1}{y_2} - {x_2}{y_1})\) vuông góc với cả hai vecto \(\overrightarrow u \) và \(\overrightarrow v \). b) Cho mặt phẳng (P). Nếu vecto \(\overrightarrow n \) khác \(\overrightarrow 0 \) và có giá vuông góc với mặt phẳng (P) thì \(\overrightarrow n \) được gọi là vecto pháp tuyến của mặt phẳng (P). Lời giải chi tiết: a) \(\overrightarrow n = (0.0 - 1.1;1.2 - 0.1;1.1 - 2.0) = ( - 1;2;1)\). b) \(\overrightarrow n \) vuông góc với cả hai vecto chỉ phương của mặt phẳng (P) nên \(\overrightarrow n \) có giá vuông góc với mặt phẳng (P) và là vecto pháp tuyến của mặt phẳng (P). LT3 Trả lời câu hỏi Luyện tập 3 trang 52 SGK Toán 12 Cánh diều Trong Ví dụ 3, vecto \(\overrightarrow {n'} = (1; - 2;1)\) có là vecto pháp tuyến của mặt phẳng (P) hay không? Vì sao? Ví dụ 3: Cho mặt phẳng (P) có cặp vecto chỉ phương là \(\overrightarrow a = (1;3;5)\), \(\overrightarrow b = ( - 3; - 1;1)\). Phương pháp giải: Tìm một vecto pháp tuyến \(\overrightarrow n \) của (P). Nếu \(\overrightarrow {n'} \) cùng phương với \(\overrightarrow n \) thì \(\overrightarrow {n'} \) là vecto pháp tuyến của mặt phẳng (P) và ngược lại. Lời giải chi tiết: Một vecto pháp tuyến của mặt phẳng (P) là: \(\overrightarrow n = \left[ {\overrightarrow a ,\overrightarrow b } \right] = \left( {\left| {\begin{array}{*{20}{c}}3&5\\{ - 1}&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}5&1\\1&{ - 3}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}1&3\\{ - 3}&{ - 1}\end{array}} \right|} \right) = \left( {8; - 16;8} \right)\). Ta có \(\overrightarrow {n'} = (1; - 2;1) = \frac{1}{8}(8; - 16;8) = \frac{1}{8}\overrightarrow n \).
|