Giải mục 3 trang 23, 24 SGK Toán 12 tập 1 - Kết nối tri thức

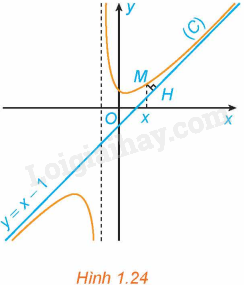
HĐ3

Trả lời câu hỏi Hoạt động 3 trang 23 SGK Toán 12 Kết nối tri thức

Cho hàm số $y = f\left( x \right) = x - 1 + \frac{2}{{x + 1}}$ có đồ thị (C) và đường thẳng $y = x - 1$ như Hình 1.24.

a) Với $x >  - 1$, xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng $y = x - 1$. Có nhận xét gì về khoảng cách MH khi $x \to  + \infty$?

b) Chứng tỏ rằng $\mathop {\lim }\limits_{x \to  + \infty } \left[ {f\left( x \right) - \left( {x - 1} \right)} \right] = 0$. Tính chất này thể hiện trên Hình 1.24 như thế nào?

Phương pháp giải:

Sử dụng kiến thức về giới hạn của hàm số để tính giới hạn.

Lời giải chi tiết:

a) Nhìn vào đồ thị ta thấy, khi $x \to  + \infty$ thì khoảng cách MH tiến tới 0.

b) Ta có: $\mathop {\lim }\limits_{x \to  + \infty } \left[ {f\left( x \right) - \left( {x - 1} \right)} \right] = \mathop {\lim }\limits_{x \to  + \infty } \left[ {x - 1 + \frac{2}{{x + 1}} - \left( {x - 1} \right)} \right] = \mathop {\lim }\limits_{x \to  + \infty } \frac{2}{{x + 1}} = \mathop {\lim }\limits_{x \to  + \infty } \frac{{\frac{2}{x}}}{{1 + \frac{1}{x}}} = 0$

Tính chất này được thể hiện trong Hình 1.24 là: Khoảng cách từ điểm M của đồ thị hàm số (C) đến đường thẳng $y = x - 1$ tiến đến 0 khi $x \to  + \infty$.

LT3

Trả lời câu hỏi Luyện tập 3 trang 24 SGK Toán 12 Kết nối tri thức

Tìm các tiệm cận đứng và tiệm cận xiên của đồ thị hàm số $y = f\left( x \right) = \frac{{{x^2} - 4x + 2}}{{1 - x}}$.

Phương pháp giải:

Sử dụng kiến thức về tìm khái niệm đường tiệm cận xiên để tìm tiệm cận xiên: Đường thẳng $y = ax + b\left( {a \ne 0} \right)$ gọi là đường tiệm cận xiên (gọi tắt là tiệm cận xiên) của đồ thị hàm số $y = f\left( x \right)$ nếu $\mathop {\lim }\limits_{x \to  + \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0$ hoặc $\mathop {\lim }\limits_{x \to  - \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0$. 

Lời giải chi tiết:

Ta có: $\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} - 4x + 2}}{{1 - x}} =  + \infty$; $\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{{x^2} - 4x + 2}}{{1 - x}} =  - \infty$

Vậy tiệm cận đứng của đồ thị hàm số $y = f\left( x \right)$ là đường thẳng $x = 1$

Ta có: $y = f\left( x \right) = \frac{{{x^2} - 4x + 2}}{{1 - x}} =  - x + 3 - \frac{1}{{1 - x}}$

Do đó, $\mathop {\lim }\limits_{x \to  + \infty } \left[ {f\left( x \right) - \left( { - x + 3} \right)} \right] = \mathop {\lim }\limits_{x \to  + \infty } \frac{{ - 1}}{{1 - x}} = 0$, $\mathop {\lim }\limits_{x \to  - \infty } \left[ {f\left( x \right) - \left( { - x + 3} \right)} \right] = \mathop {\lim }\limits_{x \to  - \infty } \frac{{ - 1}}{{1 - x}} = 0$

Vậy tiệm cận xiên của đồ thị hàm số $y = f\left( x \right)$ là đường thẳng $y =  - x + 3$