Giải mục 3 trang 34, 35, 36 SGK Toán 11 tập 2 - Kết nối tri thứcCho đường thẳng a vuông góc với mặt phẳng (P) và song song với đường thẳng b.
Lựa chọn câu để xem lời giải nhanh hơn
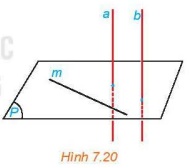
HĐ 5 Video hướng dẫn giải Cho đường thẳng a vuông góc với mặt phẳng (P) và song song với đường thẳng b. Lấy một đường thẳng m bất kì thuộc mặt phẳng (P). Tính (b, m) và từ đó rút ra mối quan hệ giữa b và (P).
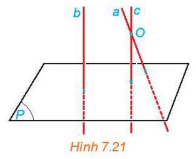
Phương pháp giải: Cho a, b là 2 đường thẳng phân biệt, nếu đường thẳng b // b’ thì (a, b) = (a, b’) Lời giải chi tiết: \(\left. \begin{array}{l}a \bot \left( P \right)\\m \subset \left( P \right)\end{array} \right\} \Rightarrow a \bot m \Rightarrow \left( {a,m} \right) = {90^0}\) a // b \( \Rightarrow \left( {a,m} \right) = \left( {b,m} \right) = {90^0}\) mà đường thẳng m bất kì thuộc mặt phẳng (P) \( \Rightarrow \) b \( \bot \) (P). HĐ 6 Video hướng dẫn giải Cho hai đường thẳng phân biệt a và b cùng vuông góc với mặt phẳng (P). Xét O là một điểm thuộc a nhưng không thuộc b. Gọi c là đường thẳng qua O và song song với b.
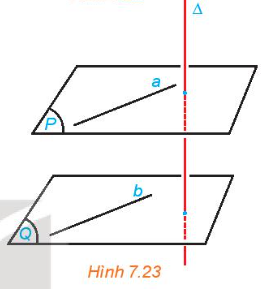
a) Hỏi c có vuông góc với (P) hay không? Nêu nhận xét về vị trí tương đối giữa a và c. b) Nêu nhận xét về vị trí tương đối giữa hai đường thẳng a và b. Phương pháp giải: - Sử dụng kết quả của hoạt động 5 trang 34. - Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng. Lời giải chi tiết: a) b // c; b \( \bot \) (P) \( \Rightarrow \) c \( \bot \) (P) Mà a \( \bot \) (P) a, c cùng đi qua điểm O \( \Rightarrow \) a trùng c. b) Ta có b // c mà a trùng c nên a // b. HĐ 7 Video hướng dẫn giải Cho hai mặt phẳng (P) và (Q) song song với nhau và đường thẳng \(\Delta \) vuông góc với (P). Gọi b là một đường thẳng bất kì thuộc (Q). Lấy một đường thẳng a thuộc (P) sao cho a song song với b (H.7.23). So sánh (\(\Delta \), b) và (\(\Delta \), a). Từ đó rút ra mối quan hệ giữa \(\Delta \) và (Q).
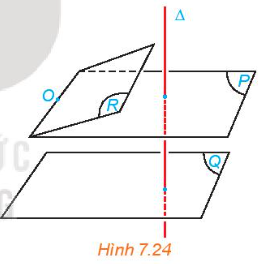
Phương pháp giải: Sử dụng định nghĩa 2 đường thẳng vuông góc và đường thẳng vuông góc với mặt phẳng. Lời giải chi tiết: \(\left. \begin{array}{l}\Delta \bot \left( P \right)\\a \subset \left( P \right)\end{array} \right\} \Rightarrow \Delta \bot a,a//b \Rightarrow \Delta \bot b \Rightarrow \left( {\Delta ,b} \right) = {90^0}\) \(\Delta \bot a \Rightarrow \left( {\Delta ,a} \right) = {90^0}\) \( \Rightarrow \) (\(\Delta \), b) = (\(\Delta \), a) mà b là đường thẳng bất kì thuộc (Q) \( \Rightarrow \) \(\Delta \bot \left( Q \right)\) HĐ 8 Video hướng dẫn giải Cho hai mặt phẳng phân biệt (P) và (Q) cùng vuông góc với đường thẳng \(\Delta \). Xét O là một điểm thuộc mặt phẳng (P) nhưng không thuộc mặt phẳng (Q). Gọi (R) là mặt phẳng đi qua O và song song với (Q) (H.7.24).
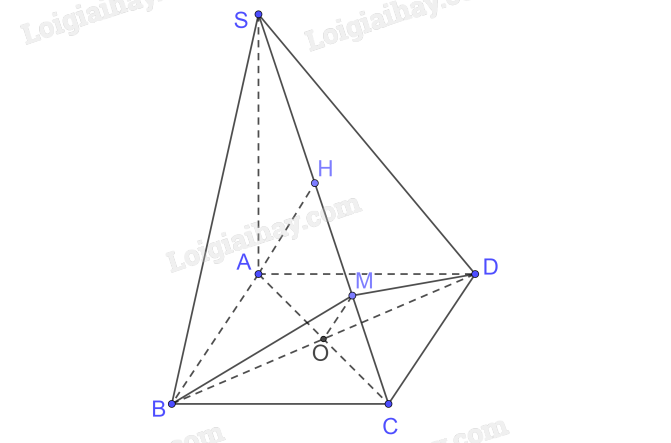
a) Hỏi (R) có vuông góc với Δ hay không? Nêu nhận xét về vị trí tương đối giữa (P) và (R). b) Nêu vị trí tương đối giữa (P) và (Q). Phương pháp giải: - Sử dụng kết quả của hoạt động 7 trang 35 - Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước. Lời giải chi tiết: a) (R) // (Q); \(\Delta \) \( \bot \) (Q) \( \Rightarrow \) \(\Delta \) \( \bot \) (R) Mà \(\Delta \) \( \bot \) (P) và (R), (Q) là 2 mặt phẳng cùng đi qua O \( \Rightarrow \) (R) trùng (P) b) (R) // (Q) mà (R) trùng (P) nên (P) // (Q) LT 3 Video hướng dẫn giải Một chiếc bàn có các chân cùng vuông góc với mặt phẳng chứa mặt bàn và mặt phẳng chứa mặt sàn. Hỏi hai mặt phẳng đó có song song với nhau hay không? Vì sao? Phương pháp giải: Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau. Lời giải chi tiết: Ta coi chân bàn như đường thẳng và mặt bàn, mặt sàn là 2 mặt phẳng. Một chiếc bàn có các chân cùng vuông góc với mặt phẳng chứa mặt bàn và mặt phẳng chứa mặt sàn nên hai mặt phẳng đó có song song với nhau vì hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau. HĐ 9 Video hướng dẫn giải Cho đường thẳng a song song với mặt phẳng (P) và đường thẳng \(\Delta \) vuông góc với mặt phẳng (P). Tính (\(\Delta \), a). Phương pháp giải: Sử dụng định nghĩa 2 đường thẳng vuông góc và đường thẳng vuông góc với mặt phẳng. Lời giải chi tiết: Vì a // (P) nên a // b sao cho b \( \subset \) (P) \( \Rightarrow \) (\(\Delta \); a) = (\(\Delta \); b) Mà \(\Delta \) \( \bot \) (P); b \( \subset \) (P) nên \(\Delta \) \( \bot \) b \( \Rightarrow \) (\(\Delta \); b) = 900 Vậy (\(\Delta \); a) = 900 HĐ 10 Video hướng dẫn giải Cho đường thẳng a và mặt phẳng (P) cùng vuông góc với một đường thẳng \(\Delta \). a) Qua một điểm O thuộc (P), kẻ đường thẳng a' song song với a. Nêu vị trí tương đối giữa a' và (P). b) Nêu vị trí tương đối giữa a và (P). Phương pháp giải: Sử dụng lý thuyết đường thẳng song song với mặt phẳng và đường thẳng vuông góc với mặt phẳng. Lời giải chi tiết: a) \(\Delta \bot a,a//a' \Rightarrow \Delta \bot a'\) \(\Delta \bot a',\Delta \bot \left( P \right)\) \( \Rightarrow \) a' // (P) hoặc a' \( \subset \) (P) mà điểm O thuộc (P) và đi qua a' Vậy a' \( \subset \) (P). b) a' // a; a' \( \subset \) (P) \( \Rightarrow \)a // (P) hoặc a \( \subset \) (P) vì a và (P) không phân biệt. LT 4 Video hướng dẫn giải Cho hình chóp S.ABCD có đáy ABCD là một hình vuông, SA \( \bot \) (ABCD). Kẻ AH vuông góc với SC (H thuộc SC), BM vuông góc với SC (M thuộc SC). Chứng minh rằng SC \( \bot \) (MBD) và AH // (MBD).
Phương pháp giải: - Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó. - Trong 1 mặt phẳng có 2 đường thẳng cùng vuông góc với đường thẳng thứ 3 thì chúng song song. - Đường thẳng song song với mặt phẳng nếu nó song song với 1 đường thẳng nằm trong mặt phẳng đó. Lời giải chi tiết: \(\begin{array}{l}\left. \begin{array}{l} + )AC \bot BD\,\,\left( {hv\,\,ABCD} \right)\\SA \bot BD\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\\AC \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow BD \bot \left( {SAC} \right)\\\left. \begin{array}{l} + )BD \bot SC\left( {BD \bot \left( {SAC} \right)} \right)\\BM \bot SC\\BD \cap BM = \left\{ B \right\}\end{array} \right\} \Rightarrow SC \bot \left( {MBD} \right)\end{array}\) Gọi \(AC \cap BD = \left\{ O \right\}\) \(\left. \begin{array}{l}SC \bot \left( {MBD} \right)\\OM \subset \left( {MBD} \right)\end{array} \right\} \Rightarrow SC \bot OM\) Mà \(AH \bot SC\) \( \Rightarrow AH//OM,OM \subset \left( {MBD} \right) \Rightarrow AH//\left( {MBD} \right)\)
|