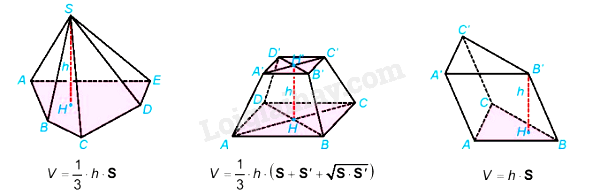
Lý thuyết Thể tích - Toán 11 Kết nối tri thứcPhần không gian được giới hạn bởi hình chóp, hình chóp cụt đều, hình lăng trụ, hình hộp tương ứng được gọi là khối chóp, khối chóp cụt đều, khối lăng trụ, khối hộp. Phần không gian được giới hạn bởi hình chóp, hình chóp cụt đều, hình lăng trụ, hình hộp tương ứng được gọi là khối chóp, khối chóp cụt đều, khối lăng trụ, khối hộp. Đỉnh, mặt, cạnh, đường cao của các khối hình đó lần lượt là đỉnh, mặt, cạnh, đường cao của hình chóp, hình chóp cụt đều, hình lăng trụ, hình hộp tương ứng. - Thể tích của khối chóp có diện tích đáy S và đường cao h là \(V = \frac{1}{3}.h.S\). - Thể tích của khối chóp cụt đều có diện tích đáy lớn S, diện tích đáy bé S’ và chiều cao h là \(V = \frac{1}{3}.h.\left( {S + S' + \sqrt {S.S'} } \right)\). - Thể tích của khối lăng trụ có diện tích đáy S và chiều cao h là \(V = h.S\).
Nhận xét: - Thể tích khối tứ diện bằng một phần ba tích của diện tích một mặt và chiều cao của khối tứ diện ứng với mặt đó. - Thể tích của khối hộp bằng tích của diện tích một mặt và chiều cao của khối hộp tương ứng với mặt đó.
|