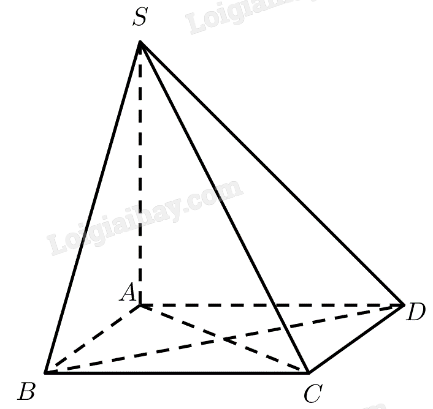
Bài 1 trang 56 SGK Toán 11 tập 2 – Chân trời sáng tạoCho hình chóp (S.ABCD) có đáy là hình thoi (ABCD) cạnh (a). Cho biết (SA = asqrt 3 ,SA bot AB) và (SA bot A{rm{D}}). Đề bài Cho hình chóp \(S.ABCD\) có đáy là hình thoi \(ABCD\) cạnh \(a\). Cho biết \(SA = a\sqrt 3 \), \(SA \bot AB\) và \(SA \bot AD\). Tính góc giữa \(SB\) và \(CD\), \(SD\) và \(C{\rm{B}}\). Phương pháp giải - Xem chi tiết Cách xác định góc giữa hai đường thẳng \(a\) và \(b\): Bước 1: Lấy một điểm \(O\) bất kì. Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\). Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\). Lời giải chi tiết a) Ta có: \(CD\parallel AB \Rightarrow \left( {SB,CD} \right) = \left( {SB,AB} \right) = \widehat {SBA}\). \(\tan \widehat {SBA} = \frac{{SA}}{{AB}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \Rightarrow \widehat {SBA} = {60^ \circ }\). Vậy \(\left( {SB,CD} \right) = {60^ \circ }\). a) Ta có: \(C{\rm{B}}\parallel AD \Rightarrow \left( {SD,C{\rm{B}}} \right) = \left( {SD,AD} \right) = \widehat {SDA}\). \(\tan \widehat {SDA} = \frac{{SA}}{{AD}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \Rightarrow \widehat {SDA} = {60^ \circ }\). Vậy \(\left( {SD,C{\rm{B}}} \right) = {60^ \circ }\).  Chia sẻ Bình luận
Group 2K9 Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
