Đề thi học kì 1 Toán 7 - Đề số 3 - Kết nối tri thứcTải vềI. TRẮC NGHIỆM ( 3 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
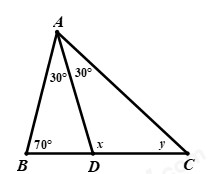
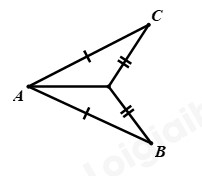
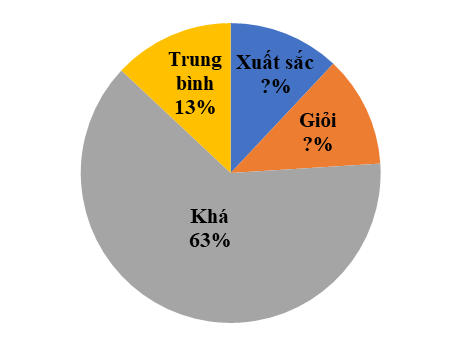
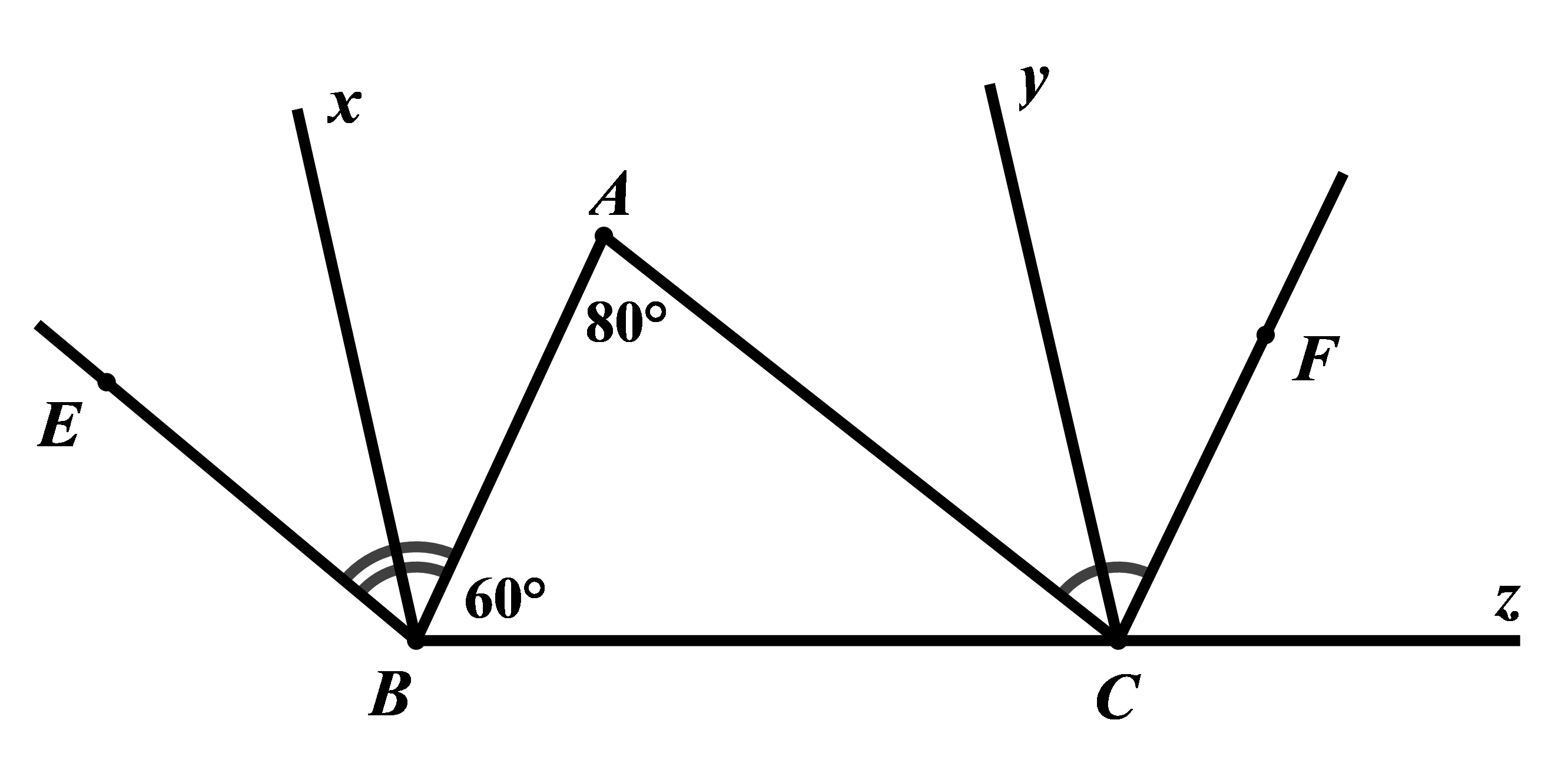
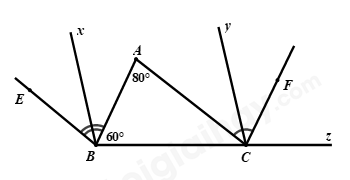
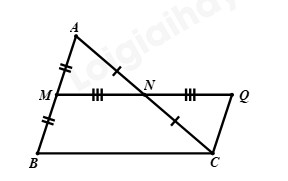
Đề bài Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm. Câu 1: Kết quả của phép tính: \(\dfrac{1}{2} + {\left[ {{{\left( { - 1103} \right)}^{1999}}} \right]^0}\) là: A. \(\dfrac{1}{2}\) B. \(1\dfrac{1}{2}\) C. \(1\) D. \(\dfrac{{ - 1}}{2}\) Câu 2: Số nào dưới đây là số vô tỉ? A. \(\sqrt 7 \) B. \(1,\left( {01} \right)\) C. \(\sqrt {16} \) D. \(\dfrac{{ - 1}}{7}\) Câu 3: Kim tự tháp Kheops là công trình kiến trúc nổi tiếng thể giới. Để xây dựng được công trình này, người ta phải sử dụng tới hơn 2,5 triệu mét khối đá, với diện tích đáy lên tới 52 198,16 \({m^2}\). (Theo khoahoc.tv) Biết rằng đáy của kim tự tháp Kheops có dạng một hình vuông. Tính độ dài cạnh đáy của kim tự tháp này (làm tròn kết quả đến chữ số thập phân thứ nhất). A. \(229,5m\) B. \(229m\) C. \(228,5m\) D. \(228m\) Câu 4: Kết quả của phép tính: \(\left| {5 - \sqrt {45} } \right| + 15 - \sqrt {45} \) là: A. \(10\) B. \(20 - 2\sqrt {45} \) C. \(20\) D. \(10 - \sqrt {45} \) Câu 5: Tính số đo của góc \(x,y\) trong hình vẽ dưới đây: A. \(x = {120^0},y = {30^0}\) B. \(x = {115^0},y = {35^0}\) C. \(x = {100^0},y = {50^0}\) D. \(x = {105^0},y = {45^0}\) Câu 6: Quan sát hình vẽ sau: Tính số đo của góc \(B\), biết \(\angle ACD = {30^0}\). A. \({30^0}\) B. \({60^0}\) C. \({25^0}\) D. \({40^0}\) Câu 7: Cho tam giác \(ABC\) và tam giác \(NPM\) có \(BC = PM,\angle B = \angle P = {90^0}\). Cần thêm một điều kiện gì để tam giác \(ABC\) và tam giác \(NPM\) bằng nhau theo trường hợp cạnh huyền – cạnh góc vuông? A. \(AB = PM\) B. \(AB = PN\) C. \(AC = MN\) D. \(\angle A = \angle N\) Câu 8: Tỉ lệ phần trăm số học sinh xuất sắc, giỏi, khá, trung bình của một lớp được biểu diễn qua biểu đồ hình quạt tròn sau: Tìm tỉ số phần trăm số học sinh xuất sắc và số hóc inh giỏi của lớp đó, biết rằng số học sinh xuất sắc bằng số học sinh giỏi. A. Số học sinh xuất sắc chiếm \(14\% \), số học sinh giỏi chiếm \(14\% \). B. Số học sinh xuất sắc chiếm \(16\% \), số học sinh giỏi chiếm \(16\% \). C. Số học sinh xuất sắc chiếm \(15\% \), số học sinh giỏi chiếm \(15\% \). D. Số học sinh xuất sắc chiếm \(12\% \), số học sinh giỏi chiếm \(12\% \). Phần II. Tự luận (7 điểm): Bài 1: (2,0 điểm) Thực hiện phép tính: a) \(\dfrac{{ - 8}}{{19}}.\dfrac{{16}}{{31}} + \dfrac{{ - 8}}{{19}}.\dfrac{{15}}{{31}} - \dfrac{{11}}{{19}}\) b) \(\sqrt {{{\left( { - 5} \right)}^2}} .{\left( { - \dfrac{1}{5}} \right)^2}:\left[ {{{\left( {\dfrac{{ - 1}}{3}} \right)}^2} + \sqrt {\dfrac{1}{4}} - \sqrt {\dfrac{{16}}{9}} } \right]\) c) \(\sqrt {121} - \sqrt {225} + \sqrt {\dfrac{{25}}{4}} \) d) \(\left| {\dfrac{{ - 11}}{3}} \right| + {\left( {\dfrac{{ - 1}}{2}} \right)^2} - \left| {4\dfrac{1}{2} + \left( { - 3,25} \right)} \right|\) Bài 2: (2,0 điểm) Tìm \(x\), biết: a) \(\left( {3{x^2} + 1} \right)\left( {4x + \dfrac{1}{3}} \right) = 0\) b) \({\left( {x - \dfrac{3}{5}} \right)^2} = \dfrac{4}{3}:\dfrac{1}{3}\) c) \(\left( {x + 2.\sqrt {16} } \right).\left| {2x + 3} \right| = 0\) d) \(\left| {x - \dfrac{2}{3}} \right| - 0,75 = 1\dfrac{1}{4}\) Bài 3: (1,0 điểm) Trong hình vẽ bên dưới có \(BE//AC,CF//AB\). Biết \(\angle A = {80^0},\angle ABC = {60^0}.\) a) Chứng minh rằng \(\angle ABE = \angle ACF\); b) Tính số đo của các góc \(BCF\) và \(ACB\). c) Gọi \(Bx,Cy\) lần lượt là tia phân giác của các góc \(ABE\) và \(ACF\). Chứng minh rằng \(Bx//Cy\). Bài 4: (1,5 điểm) Cho tam giác \(ABC\) nhọn, lấy điểm \(M\) là trung điểm của cạnh \(AB\), lấy điểm \(N\) là trung điểm của cạnh \(AC\). Trên tia đối của tia \(NM\) lấy điểm \(Q\) sao cho \(NM = NQ\). Chứng minh rằng: a) Hai tam giác \(AMN,CQN\) bằng nhau; b) \(MB\) song song với \(QC\); c) \(MN = \dfrac{1}{2}BC\). Bài 5: (0,5 điểm) Tìm giá trị nhỏ nhất của biểu thức: \(A = \sqrt {{{(x + 2)}^4} + 25} + {\left( {1 - y} \right)^2} - 999\) Lời giải Phần I: Trắc nghiệm
Câu 1. Phương pháp: Sử dụng quy ước: \({a^0} = 1\) với \(a \ne 0\) Thực hiện phép cộng với số hữu tỉ. Cách giải: \(\dfrac{1}{2} + {\left[ {{{\left( { - 1103} \right)}^{1999}}} \right]^0}\)\( = \dfrac{1}{2} + 1 = 1\dfrac{1}{2}\) Chọn B. Câu 2. Phương pháp: Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn. Cách giải: Ta có: \(1,\left( {01} \right)\) là số thập phân vô hạn tuần hoàn \(\sqrt {16} = 4\) không phải là số vô tỉ \(\dfrac{{ - 1}}{7}\) là số hữu tỉ. Do đó, \(\sqrt 7 \) là số vô tỉ. Chọn A. Câu 3. Phương pháp: Gọi độ dài cạnh hình vuông là \(x\,\,\left( {x > 0} \right)\,\,\left( m \right)\) Tính căn bậc hai số học của \(x\) là độ dài cạnh đáy của kim tự tháp cần tìm. Cách giải: Gọi độ dài cạnh hình vuông là \(x\,\,\left( {x > 0} \right)\,\,\left( m \right)\) Theo giả thiết, ta có: \({x^2} = 52\,198,16 \Rightarrow x = \sqrt {52198,16} = 228,469...\) \( \Rightarrow x \approx 228,5\,\,\left( m \right)\) Vậy độ dài cạnh đáy của kim tự tháp xấp xỉ 228,5m. Chọn C. Câu 4. Phương pháp: Vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,\,\,\,khi\,\,\,x > 0\\ - x\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,khi\,\,\,x = 0\end{array} \right.\) Cách giải: Ta có: \(5 = \sqrt {{5^2}} = \sqrt {25} \) Vì \(25 < 45\) nên \(\sqrt {25} < \sqrt {45} \) do đó, \(5 < \sqrt {45} \) Suy ra \(5 - \sqrt {45} < 0\) Do đó, \(\left| {5 - \sqrt {45} } \right| = - \left( {5 - \sqrt {45} } \right) = - 5 + \sqrt {45} \) Ta có: \(\left| {5 - \sqrt {45} } \right| + 15 - \sqrt {45} \) \(\begin{array}{l} = - 5 + \sqrt {45} + 15 - \sqrt {45} \\ = 10\end{array}\) Chọn A. Câu 5. Phương pháp: Áp dụng định lý góc ngoài của tam giác: góc ngoài của tam giác bằng tổng hai góc trong không kề với nó, tính số đo của \(x\). Áp dụng định lý tổng ba góc trong một tam giác, tính số đo của \(y.\) Cách giải: *Tam giác \(ABD\) có \(\angle ADC\) là góc ngoài tại đỉnh \(D\), ta có: \(\angle ADC = \angle BAD + \angle ABD\) (góc ngoài của tam giác bằng tổng hai góc trong không kề với nó) \(\begin{array}{l} \Rightarrow \angle ADC = {30^0} + {70^0} = {100^0}\\ \Rightarrow x = {100^0}\end{array}\) *Xét tam giác \(ACD\) có: \(\angle DAC + \angle ADC + \angle ACD = {180^0}\) (định lý tổng ba góc trong một tam giác) \(\begin{array}{l} \Rightarrow {30^0} + {100^0} + y = {180^0}\\ \Rightarrow {130^0} + y = {180^0}\\ \Rightarrow y = {180^0} - {130^0}\\ \Rightarrow y = {50^0}\end{array}\) Vậy \(x = {100^0},y = {50^0}\) Chọn C. Câu 6. Phương pháp: Vận dụng định lí: Nếu ba cạnh của tam giác bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau. Cách giải: Xét \(\Delta ADC\) và \(\Delta ADB\) có: \(AC = AB\) (giả thiết) \(CD = BD\) (giả thiết) \(AD\) là cạnh chung Suy ra \(\Delta ADC = \Delta ADB\,\left( {c.c.c} \right)\) Do đó, \(\angle ACD = \angle ABD\) (hai góc tương ứng) Mà \(\angle ACD = {30^0}\) nên \(\angle ABD = \angle B = {30^0}\) Chọn A. Câu 7. Phương pháp: Áp dụng định lý: Nếu cạnh huyền và một cạnh góc vuông của tam giác này bằng cạnh huyền và một cạnh của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. Cách giải: Hai tam giác \(ABC\) và \(NPM\) có \(BC = PM,\angle B = \angle P = {90^0}\) mà \(BC,PM\) lầm lượt là hai cạnh góc vuông của hai tam giác \(ABC\) và \(NPM\) nên để hai tam giác bằng nhau theo trường hợp cạnh huyền – cạnh góc vuông thì ta cần thêm hai cạnh huyền bằng nhau là \(AC = MN\). Chọn C. Câu 8. Phương pháp: Đọc và phân tích dữ liệu của biểu đồ hình quạt tròn. Cách giải: Gọi số phần trăm học sinh xuất sắc là \(x\% \) (điều kiện: \(x > 0\)). Vì số học sinh xuất sắc bằng số học sinh giỏi nên số phần trăm học sinh giỏi là \(x\% \) (điều kiện: \(x > 0\)). Ta có: \(\begin{array}{l}x + x + 63\% + 13\% = 100\% \\2x + 76\% = 100\% \\2x = 100\% - 76\% \\2x = 24\% \\x = 24\% :2\\x = 12\% \end{array}\) Vậy số học sinh xuất sắc chiếm \(12\% \), số học sinh giỏi chiếm \(12\% \). Chọn D.
Phần II. Tự luận: Bài 1. Phương pháp: a) Thực hiện các phép toán với số hữu tỉ. b) Tính căn bậc hai của một số. Lũy thừa của một số hữu tỉ: \({\left( {\dfrac{a}{b}} \right)^n} = \dfrac{{{a^n}}}{{{b^n}}}\,\,\left( {b \ne 0;n \in \mathbb{Z}} \right)\). Thực hiện các phép toán với số hữu tỉ. c) Thực hiện tính căn bậc hai của một số. d) Vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,\,\,\,khi\,\,\,x > 0\\ - x\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,khi\,\,\,x = 0\end{array} \right.\) Thực hiện các phép toán với số hữu tỉ. Cách giải: a) \(\dfrac{{ - 8}}{{19}}.\dfrac{{16}}{{31}} + \dfrac{{ - 8}}{{19}}.\dfrac{{15}}{{31}} - \dfrac{{11}}{{19}}\) \(\begin{array}{l} = \dfrac{{ - 8}}{{19}}.\left( {\dfrac{{16}}{{31}} + \dfrac{{15}}{{31}}} \right) - \dfrac{{11}}{{19}}\\ = \dfrac{{ - 8}}{{19}}.\dfrac{{31}}{{31}} - \dfrac{{11}}{{19}}\\ = \dfrac{{ - 8}}{{19}}.1 - \dfrac{{11}}{{19}}\\ = \dfrac{{ - 19}}{{19}} = - 1\end{array}\) b) \(\sqrt {{{\left( { - 5} \right)}^2}} .{\left( { - \dfrac{1}{5}} \right)^2}:\left[ {{{\left( {\dfrac{{ - 1}}{3}} \right)}^2} + \sqrt {\dfrac{1}{4}} - \sqrt {\dfrac{{16}}{9}} } \right]\) \(\begin{array}{l} = 5.\dfrac{{{{\left( { - 1} \right)}^2}}}{{{5^2}}}:\left[ {\dfrac{{{{\left( { - 1} \right)}^2}}}{{{3^2}}} + \dfrac{1}{2} - \dfrac{4}{3}} \right]\\ = 5.\dfrac{1}{{{5^2}}}:\left( {\dfrac{1}{9} + \dfrac{1}{2} - \dfrac{4}{3}} \right)\\ = \dfrac{1}{5}:\left( {\dfrac{2}{{18}} + \dfrac{9}{{18}} - \dfrac{{24}}{{18}}} \right)\\ = \dfrac{1}{5}:\dfrac{{ - 13}}{{18}}\\ = \dfrac{1}{5}.\dfrac{{18}}{{ - 13}}\\ = \dfrac{{18}}{{ - 65}}\end{array}\) c) \(\sqrt {121} - \sqrt {225} + \sqrt {\dfrac{{25}}{4}} \) \(\begin{array}{l} = 11 - 15 + \dfrac{5}{2}\\ = - 4 + \dfrac{5}{2} = \dfrac{{ - 8}}{2} + \dfrac{5}{2}\\ = \dfrac{{ - 3}}{2}\end{array}\) d) \(\left| {\dfrac{{ - 11}}{3}} \right| + {\left( {\dfrac{{ - 1}}{2}} \right)^2} - \left| {4\dfrac{1}{2} + \left( { - 3,25} \right)} \right|\) \(\begin{array}{l} = - \left( {\dfrac{{ - 11}}{3}} \right) + \dfrac{{{{\left( { - 1} \right)}^2}}}{{{2^2}}} - \left| {\dfrac{9}{2} - \dfrac{{13}}{4}} \right|\\ = \dfrac{{11}}{3} + \dfrac{1}{4} - \left| {\dfrac{{18}}{4} - \dfrac{{13}}{4}} \right|\\ = \dfrac{{11}}{3} + \dfrac{1}{4} - \left| {\dfrac{5}{4}} \right|\\ = \dfrac{{11}}{3} + \dfrac{1}{4} - \dfrac{5}{4}\\ = \dfrac{{11}}{3} - \dfrac{4}{4} = \dfrac{{11}}{3} - 1\\ = \dfrac{{11}}{3} - \dfrac{3}{3} = \dfrac{8}{3}\end{array}\) Bài 2. Phương pháp: a) Giải: \(A\left( x \right).B\left( x \right) = 0\) Trường hợp 1: Giải \(A\left( x \right) = 0\) Trường hợp 2: Giải \(B\left( x \right) = 0\) b) Giải \({\left[ {A\left( x \right)} \right]^2} = {a^2} = {\left( { - a} \right)^2}\) Trường hợp 1: \(A\left( x \right) = a\) Trường hợp 2: \(A\left( x \right) = - a\) c) Giải: \(A\left( x \right).B\left( x \right) = 0\) Trường hợp 1: Giải \(A\left( x \right) = 0\) Trường hợp 2: Giải \(B\left( x \right) = 0\) Vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,\,\,\,khi\,\,\,x > 0\\ - x\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,khi\,\,\,x = 0\end{array} \right.\) d) vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,\,\,\,khi\,\,\,x > 0\\ - x\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,khi\,\,\,x = 0\end{array} \right.\) Cách giải: a) \(\left( {3{x^2} + 1} \right)\left( {4x + \dfrac{1}{3}} \right) = 0\) Trường hợp 1: \(3{x^2} + 1 = 0\) Vì \({x^2} \ge 0\) với mọi \(x\) nên \(3{x^2} \ge 0\) với mọi \(x\) Do đó, \(3{x^2} + 1 \ge 1 > 0\) với mọi \(x\) Vậy không có \(x\) thỏa mãn \(3{x^2} + 1 = 0\). Trường hợp 2: \(\begin{array}{l}4x + \dfrac{1}{3} = 0\\4x = \dfrac{{ - 1}}{3}\\x = \dfrac{{ - 1}}{3}:4 = \dfrac{{ - 1}}{3}.\dfrac{1}{4}\\x = \dfrac{{ - 1}}{{12}}\end{array}\) Vậy \(x = \dfrac{{ - 1}}{{12}}\) b) \({\left( {x - \dfrac{3}{5}} \right)^2} = \dfrac{4}{3}:\dfrac{1}{3}\) \(\begin{array}{l}{\left( {x - \dfrac{3}{5}} \right)^2} = \dfrac{4}{3}.\dfrac{3}{1} = 4\\{\left( {x - \dfrac{3}{5}} \right)^2} = {2^2} = {\left( { - 2} \right)^2}\end{array}\) Trường hợp 1: \(\begin{array}{l}x - \dfrac{3}{5} = 2\\x = 2 + \dfrac{3}{5}\\x = \dfrac{{10}}{5} + \dfrac{3}{5}\\x = \dfrac{{13}}{5}\end{array}\) Vậy \(x \in \left\{ {\dfrac{{13}}{5};\dfrac{{ - 7}}{5}} \right\}\) Trường hợp 2: \(\begin{array}{l}x - \dfrac{3}{5} = - 2\\x = - 2 + \dfrac{3}{5}\\x = \dfrac{{ - 10}}{5} + \dfrac{3}{5}\\x = \dfrac{{ - 7}}{5}\end{array}\) c) \(\left( {x + 2.\sqrt {16} } \right).\left| {2x + 3} \right| = 0\) Trường hợp 1: \(\begin{array}{l}x + 2.\sqrt {16} = 0\\x + 2.4 = 0\\x + 8 = 0\\x = - 8\end{array}\) Trường hợp 2: \(\begin{array}{l}\left| {2x + 3} \right| = 0\\2x + 3 = 0\\2x = - 3\\x = - 3:2\\x = \dfrac{{ - 3}}{2}\end{array}\) Vậy \(x \in \left\{ { - 8;\dfrac{{ - 3}}{2}} \right\}\) d) \(\left| {x - \dfrac{2}{3}} \right| - 0,75 = 1\dfrac{1}{4}\) \(\begin{array}{l}\left| {x - \dfrac{2}{3}} \right| - \dfrac{3}{4} = \dfrac{5}{4}\\\left| {x - \dfrac{2}{3}} \right| = \dfrac{5}{4} + \dfrac{3}{4}\\\left| {x - \dfrac{2}{3}} \right| = \dfrac{8}{4} = 2\end{array}\) Trường hợp 1: \(\begin{array}{l}x - \dfrac{2}{3} = 2\\x = 2 + \dfrac{2}{3}\\x = \dfrac{6}{3} + \dfrac{2}{3}\\x = \dfrac{8}{3}\end{array}\) Trường hợp 2: \(\begin{array}{l}x - \dfrac{2}{3} = - 2\\x = - 2 + \dfrac{2}{3}\\x = \dfrac{{ - 6}}{3} + \dfrac{2}{3}\\x = \dfrac{{ - 4}}{3}\end{array}\) Vậy \(x \in \left\{ {\dfrac{8}{3};\dfrac{{ - 4}}{3}} \right\}\) Bài 3. Phương pháp: a) Vận dụng tính chất của hai đường thẳng song song. b) Hai góc kề bù có tổng số đo bằng \({180^0}\). Vận dụng định lý tổng ba góc trong một tam giác. c) Vận dụng dấu hiệu nhận biết của hai đường thẳng song song. Cách giải: a) Vì \(BE//AC\) (giả thiết) nên \(\angle ABE = \angle BAC\) (hai góc so le trong) Vì \(AB//CF\) (giả thiết) nên \(\angle ACF = \angle BAC\) (hai góc so le trong) Suy ra \(\angle ABE = \angle ACF\) (vì cùng bằng \(\angle BAC\)) b) Vì \(AB//CF\) (giả thiết) nên \(\angle ABC = \angle FCx = {60^0}\) (hai góc đồng vị) Ta có \(\angle BCF\) và \(\angle FCx\) là hai góc kề bù nên \(\angle BCF + \angle FCx = {180^0}\) \(\begin{array}{l} \Rightarrow \angle BCF + {60^0} = {180^0}\\ \Rightarrow \angle BCF = {180^0} - {60^0} = {120^0}\end{array}\) Xét tam giác \(ABC\) có: \(\angle BAC + \angle ABC + \angle BCA = {180^0}\) (định lí tổng ba góc trong một tam giác) \(\begin{array}{l} \Rightarrow {80^0} + {60^0} + \angle ACB = {180^0}\\ \Rightarrow {140^0} + \angle ACB = {180^0}\\ \Rightarrow \angle ACB = {180^0} - {140^0} = {40^0}\end{array}\) Vậy \(\angle BCF = {120^0},\angle ACB = {40^0}\). c) Ta có: \(Bx\) là tia phân giác của \(\angle ABE\) (giả thiết) suy ra \(\angle ABx = \dfrac{{\angle ABE}}{2} = \dfrac{{{{80}^0}}}{2} = {40^0}\) (tính chất tia phân giác của một góc) \(Cy\) là tia phân giác của \(\angle ACF\) (giả thiết) suy ra \(\angle FCy = \dfrac{{ACF}}{2} = \dfrac{{{{80}^0}}}{2} = {40^0}\) (tính chất tia phân giác của một góc) Ta có: \(\angle xAB\) và \(\angle ABC\) là hai góc kề nhau nên \(\angle BCx = \angle xAB + \angle ABC = {40^0} + {60^0} = {100^0}\) \(\angle yCF\) và \(\angle FCz\) là hai góc kề nhau nên \(\angle yCz = \angle yCF + \angle FCz = {40^0} + {60^0} = {100^0}\) Vì \(\angle BCx = \angle yCz = {100^0}\) mà hai góc này ở vị trí đồng vị nên \(Bx//Cy\) (dấu hiệu nhận biết hai đường thẳng song song). Bài 4. Phương pháp: a) Vận dụng định lý: Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau theo trường hợp cạnh – góc – cạnh (c.g.c). b) Vận dụng dấu hiệu nhận biết của hai đường thẳng song song. c) Vận dụng định lý: Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau theo trường hợp cạnh – góc – cạnh (c.g.c). Vận dụng tính chất trung điểm của đoạn thẳng, tính chất bắc cầu. Cách giải: a) Vì \(N\) là trung điểm của \(AC\) nên \(AN = NC\) Xét \(\Delta AMN\) và \(\Delta CQN\) có: \(AN = NC\) (chứng minh trên) \(\angle ANM = \angle CNQ\) (hai góc đối đỉnh) \(NM = NQ\) (giả thiết) Suy ra \(\Delta AMN = \Delta CQN\,\left( {c.g.c} \right)\) b) Vì \(\Delta AMN = \Delta CQN\) (chứng minh a), suy ra \(\angle MAN = \angle QCN\) (hai góc tương ứng) Mà hai góc này ở vị trí so le trong nên \(AM//QC\) Suy ra \(MB//QC\) (điều phải chứng minh) c) Vì \(\Delta AMN = \Delta CQN\) (chứng minh a), suy ra \(MA = QC\) (hai cạnh tương ứng) Lại có, \(M\) là trung điểm của \(AB\) nên \(MA = MB\) Suy ra, \(MB = QC\) (vì cùng bằng \(MA\)) Vì \(MB//QC\) (chứng minh b) nên \(\angle BMC = \angle QCM\) (hai góc so le trong) Xét \(\Delta BMC\) và \(\Delta QCM\) có: \(MB = QC\) (chứng minh trên) \(\angle BMC = \angle QCM\) (chứng minh trên) \(MC\) là cạnh chung Suy ra \(\Delta BMC = \Delta QCM\,\left( {c.g.c} \right)\)\( \Rightarrow BC = QM\) (hai cạnh tương ứng) Vì \(NM = NQ \Rightarrow MN = \dfrac{1}{2}MQ\). Do đó, \(MN = \dfrac{1}{2}BC\) (điều phải chứng minh) Bài 5. Phương pháp: Vận dụng kiến thức lũy thừa của một số và căn bậc hai số học của một số. Cách giải: \(A = \sqrt {{{(x + 2)}^4} + 25} + {\left( {1 - y} \right)^2} - 999\) Ta có: \(\begin{array}{l}{\left( {x + 2} \right)^4} \ge 0,\forall x \in \mathbb{R} \Rightarrow \sqrt {{{\left( {x + 2} \right)}^4} + 25} \ge \sqrt {25} = 5,\forall x \in \mathbb{R};\\{\left( {1 - y} \right)^2} \ge 0,\forall y \in \mathbb{R}\\ \Rightarrow \sqrt {{{\left( {x + 2} \right)}^4} + 25} + {\left( {1 - y} \right)^2} - 999 \ge 5 + 0 - 999 = - 994,\forall x,y \in \mathbb{R}\end{array}\) Dấu “=” xảy ra khi và chỉ khi \( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x + 2 = 0}\\{1 - y = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = - 2}\\{y = 1}\end{array}} \right.\). Vậy giá trị nhỏ nhất của \(A\) là \( - 994\) khi \(x = - 2;y = 1\) Phương pháp giải:
|