Đề thi học kì 1 Toán 7 Kết nối tri thức - Đề số 16Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:Đề bài
I. Trắc nghiệm
Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Trong các số sau, số nào là số vô tỉ?
Câu 2 :
Giá trị tuyệt đối của \(\frac{{ - 15}}{{19}}\) là:
Câu 3 :
Kết quả làm tròn số 2,4379 đến chữ số thập phân thứ ba là:
Câu 5 :
Cho \(\Delta MNP = \Delta DHK\). Khẳng định nào sau đây là đúng:
Câu 6 :
Cho tam giác ABC cân tại A, khẳng định nào sau đây SAI?
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Trong các số sau, số nào là số vô tỉ?
Đáp án : A Phương pháp giải :
Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn. Lời giải chi tiết :
Các số \(\frac{{ - 13}}{9}\); 0; 2023 là các số hữu tỉ, không là các số số tỉ. Chỉ có số \(\sqrt 3 \) là số vô tỉ. Đáp án A
Câu 2 :
Giá trị tuyệt đối của \(\frac{{ - 15}}{{19}}\) là:
Đáp án : C Phương pháp giải :
Sử dụng kiến thức giá trị tuyệt đối của một số thực: |a| = a nếu a \( \ge \) 0. |a| = -a nếu a < 0. Lời giải chi tiết :
Giá trị tuyệt đối của \(\frac{{ - 15}}{{19}}\) là: \(\left| {\frac{{ - 15}}{{19}}} \right| = \frac{{15}}{{19}}\). Đáp án C
Câu 3 :
Kết quả làm tròn số 2,4379 đến chữ số thập phân thứ ba là:
Đáp án : D Phương pháp giải :
Áp dụng quy tắc Làm tròn số thập phân dương: - Đối với chữ số hàng làm tròn: + Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5; + Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5. - Đối với chữ số sau hàng làm tròn: + Bỏ đi nếu ở phần thập phân; + Thay bằng các chữ số 0 nếu ở phần số nguyên. Lời giải chi tiết :
Số 2,4379 làm tròn đến chữ số thập phân thứ ba là 2,438 (vì 9 > 5). Đáp án D
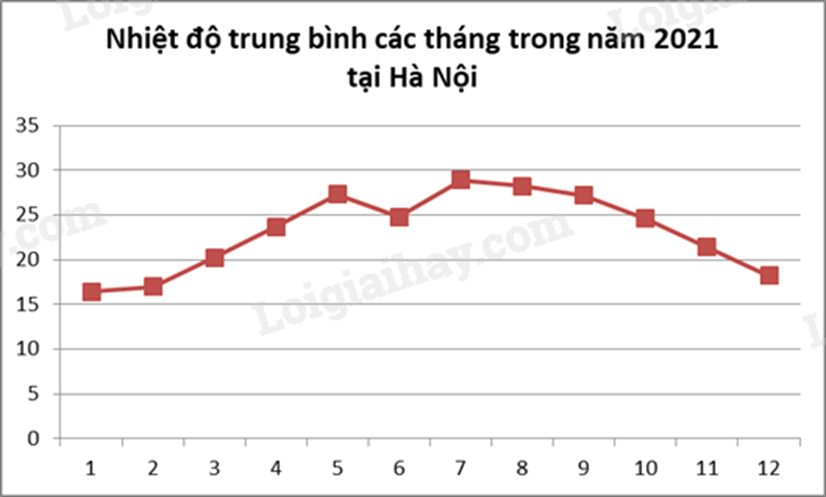
Đáp án : C Phương pháp giải :
Quan sát biểu đồ, vị trí nào cao nhất thì tháng đó có nhiệt độ cao nhất. Lời giải chi tiết :
Quan sát biểu đồ ta thấy điểm biểu diễn ở vị trí tháng 7 là cao nhất nên nhiệt độ trung bình tháng 7 cao nhất. Đáp án C
Câu 5 :
Cho \(\Delta MNP = \Delta DHK\). Khẳng định nào sau đây là đúng:
Đáp án : D Phương pháp giải :
Hai tam giác bằng nhau thì các cạnh và các góc tương ứng của chúng bằng nhau. Lời giải chi tiết :
Vì \(\Delta MNP = \Delta DHK\) nên ta có: \(MN = DH;MP = DK;NP = HK\); \(\widehat M = \widehat D;\widehat N = \widehat H;\widehat P = \widehat K\). Do đó A sai; B sai; C sai; D đúng. Đáp án D
Câu 6 :
Cho tam giác ABC cân tại A, khẳng định nào sau đây SAI?
Đáp án : A Phương pháp giải :
Tam giác cân thì hai cạnh bên bằng nhau và hai góc kề đáy bằng nhau. Tổng ba góc của một tam giác là \(180^\circ \). Lời giải chi tiết :
Tam giác ABC cân tại A thì \(\widehat B = \widehat C\); \(AB = AC\) nên khẳng định B, C đúng. Tam giác ABC có \(\widehat A + \widehat B + \widehat C = 180^\circ \), \(\widehat B = \widehat C\) nên \(\widehat A + 2\widehat B = 180^\circ \), suy ra \(2\widehat B = 180^\circ - \widehat A\), do đó \(\widehat B = \frac{{180^\circ - \widehat A}}{2}\) nên khẳng định D đúng. Đáp án A
II. Tự luận
Phương pháp giải :
Áp dụng quy tắc cộng, trừ, nhân, chia với số thực. b) Sử dụng kiến thức về bình phương của một số, căn bậc hai số học và giá trị tuyệt đối của một số thực. Lời giải chi tiết :
a) \( - 0,5 + \frac{3}{4} = - \frac{1}{2} + \frac{3}{4} = \frac{{ - 2 + 3}}{4} = \frac{1}{4}\). b) \({\left( { - \frac{2}{3}} \right)^2}.\frac{9}{{16}} + \sqrt {\frac{4}{{81}}} :\frac{{16}}{9} - \left| { - \frac{9}{{16}}} \right|.\frac{2}{3}\) \(\begin{array}{l} = \frac{4}{9}.\frac{9}{{16}} + \frac{2}{9}.\frac{9}{{16}} - \frac{9}{{16}}.\frac{2}{3}\\ = \frac{9}{{16}}.\left( {\frac{4}{9} + \frac{2}{9} - \frac{2}{3}} \right)\\ = \frac{9}{{16}}.0 = 0\end{array}\) Phương pháp giải :
Kết hợp chuyển vế và thực hiện phép tính để tìm x. b) Ta cần chia hai trường hợp: \(\left| A \right| = B\) thì A = B hoặc A = -B. Lời giải chi tiết :
a) \(\frac{4}{3} + x = \frac{{ - 1}}{6}\) \(\begin{array}{l}x = \frac{{ - 1}}{6} - \frac{4}{3}\\x = \frac{{ - 1 - 8}}{6}\\x = \frac{{ - 3}}{2}\end{array}\) Vậy \(x = \frac{{ - 3}}{2}\). b) \(2\left| {\frac{4}{5} - 2x} \right| + \frac{3}{5} = 3\) \(\begin{array}{l}2\left| {\frac{4}{5} - 2x} \right| = 3 - \frac{3}{5}\\2\left| {\frac{4}{5} - 2x} \right| = \frac{{12}}{5}\\\left| {\frac{4}{5} - 2x} \right| = \frac{{12}}{5}:2\\\left| {\frac{4}{5} - 2x} \right| = \frac{6}{5}\\\frac{4}{5} - 2x = \pm \frac{6}{5}\end{array}\) +) TH1: \(\frac{4}{5} - 2x = \frac{6}{5}\) \(\begin{array}{l}2x = \frac{4}{5} - \frac{6}{5}\\2x = \frac{{ - 2}}{5}\\x = \frac{{ - 2}}{5}:2\\x = \frac{{ - 1}}{5}\end{array}\) +) TH2: \(\frac{4}{5} - 2x = - \frac{6}{5}\) \(\begin{array}{l}2x = \frac{4}{5} + \frac{6}{5}\\2x = 2\\x = 2:2\\x = 1\end{array}\) Vậy \(x \in \left\{ {\frac{{ - 1}}{5};1} \right\}\) Phương pháp giải :
a) Cách vẽ biểu đồ hình quạt tròn: + Vẽ 1 đường tròn + Tính số đo góc của hình quạt biểu diễn từng đối tượng: 1% tương ứng với 3,6 độ. + Đo góc và chia hình tròn thành các hình quạt có số đo tương ứng + Điền số phần trăm tương ứng vào từng hình quạt, tô màu và viết chú thích, đặt tên cho biểu đồ. b) Tính m% của một số a theo công thức: \(m\% .a\). Lời giải chi tiết :
a) Số đo góc của hình quạt biểu diễn từng đối tượng là:
Ta được biểu đồ hình quạt tròn như sau: b) Số học sinh thích chơi đá cầu là: \(15\% .320 = 48\) (học sinh) Phương pháp giải :
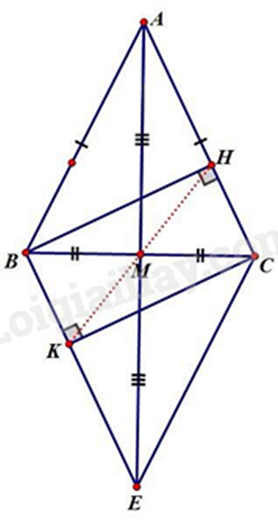
a) Chứng minh \(\Delta ABM = \Delta ACM\) theo trường hợp cạnh cạnh cạnh. b) Từ \(\Delta ABM = \Delta ACM\) suy ra \(\widehat {AMB} = \widehat {AMC}\) và hai góc này là hai góc kề bù suy ra \(AM \bot BC\). c) Chứng minh \(\Delta AMC = \Delta EMB\) nên \(\widehat {ACM} = \widehat {EBM}\), suy ra AC // BE. Chứng minh MH = MK và H, M, K thẳng hàng nên M là trung điểm của HK. Lời giải chi tiết :
a) Xét \(\Delta ABM\) và \(\Delta ACM\) có: AB = AC (gt) BM = CM (M là trung điểm của BC) AM chung Suy ra \(\Delta ABM = \Delta ACM\) (c.c.c) b) Vì \(\Delta ABM = \Delta ACM\) nên \(\widehat {AMB} = \widehat {AMC}\) (hai góc tương ứng). Mà hai góc này là hai góc kề bù nên \(\widehat {AMB} + \widehat {AMC} = 180^\circ \) Suy ra \(\widehat {AMB} + \widehat {AMB} = 180^\circ \), do đó \(\widehat {AMB} = 90^\circ \) hay \(AM \bot BC\). c) +) Xét \(\Delta AMC\) và \(\Delta EMB\) có: MA = ME (gt) \(\widehat {AMC} = \widehat {EMB}\left( { = 90^\circ } \right)\) \(BM = CM\) Suy ra \(\Delta AMC = \Delta EMB\) (hai cạnh góc vuông) nên \(\widehat {ACM} = \widehat {EBM}\) (hai góc tương ứng). Mà hai góc này ở vị trí so le trong nên AC // BE. +) Xét \(\Delta BHC\) và \(\Delta CKB\) có: \(\widehat {BHC} = \widehat {CKB}\left( { = 90^\circ } \right)\) \(\widehat {HCB} = \widehat {KBC}\) (cmt) BC chung suy ra \(\Delta BHC = \Delta CKB\) (cạnh huyền – góc nhọn) suy ra \(BH = CK;\widehat {HBC} = \widehat {KCB}\) (hai cạnh và hai góc tương ứng) Xét \(\Delta BMH\) và \(\Delta CMK\) có: \(BH = CK\) (cmt) \(\widehat {HBM} = \widehat {KCM}\) (cmt) \(BM = CM\) Suy ra \(\Delta BMH = \Delta CMK\) (c.g.c) Do đó MH = MK (1) và \(\widehat {BMH} = \widehat {CMK}\)(hai cạnh và hai góc tương ứng) Mà \(\widehat {BMH} + \widehat {HMC} = 180^\circ \) (hai góc kề bù) nên \(\widehat {CMK} + \widehat {HMC} = 180^\circ \), do đó H, M, K thẳng hàng. (2) Từ (1) và (2) suy ra M là trung điểm của HK. Phương pháp giải :
Tính 9A. Xét 9A – A. Từ đó chứng minh được \(A < \frac{3}{8}\). Lời giải chi tiết :
Ta có: \(\begin{array}{c}9A = 9\left( {\frac{1}{3} + \frac{1}{{{3^3}}} + \frac{1}{{{3^5}}} + \frac{1}{{{3^7}}} + ... + \frac{1}{{{3^{2023}}}}} \right)\\ = 3 + \frac{1}{3} + \frac{1}{{{3^3}}} + \frac{1}{{{3^5}}} + ... + \frac{1}{{{3^{2021}}}}\end{array}\) Xét \(9A - A = \left( {3 + \frac{1}{3} + \frac{1}{{{3^3}}} + \frac{1}{{{3^5}}} + ... + \frac{1}{{{3^{2021}}}}} \right) - \left( {\frac{1}{3} + \frac{1}{{{3^3}}} + \frac{1}{{{3^5}}} + \frac{1}{{{3^7}}} + ... + \frac{1}{{{3^{2023}}}}} \right)\) \(\begin{array}{c}8A = 3 + \frac{1}{3} + \frac{1}{{{3^3}}} + \frac{1}{{{3^5}}} + ... + \frac{1}{{{3^{2021}}}} - \frac{1}{3} - \frac{1}{{{3^3}}} - \frac{1}{{{3^5}}} - \frac{1}{{{3^7}}} - ... - \frac{1}{{{3^{2023}}}}\\8A = 3 + \left( {\frac{1}{3} - \frac{1}{3}} \right) + \left( {\frac{1}{{{3^3}}} - \frac{1}{{{3^3}}}} \right) + ... + \left( {\frac{1}{{{3^{2021}}}} - \frac{1}{{{3^{2021}}}}} \right) - \frac{1}{{{3^{2023}}}}\end{array}\) \(8A = 3 - \frac{1}{{{3^{2023}}}}\) \(A = \frac{3}{8} - \frac{1}{{{{8.3}^{2023}}}}\) Vì \(\frac{1}{{{{8.3}^{2023}}}} > 0\) nên \(A = \frac{3}{8} - \frac{1}{{{{8.3}^{2023}}}} < \frac{3}{8}\) Vậy \(A < \frac{3}{8}\)
|