Đề thi giữa kì 2 Toán 11 Kết nối tri thức - Đề số 4Phần trắc nghiệm (7 điểm) Câu 1: Khẳng định nào sau đây là đúng?Đề bài
I. Trắc nghiệm
Câu 1 :
Khẳng định nào sau đây là đúng?
Câu 2 :
Chọn đáp án đúng. Cho số thực a và số nguyên dương n \(\left( {n \ge 2} \right)\). Số b được gọi là căn bậc n của số a nếu:
Câu 3 :
Chọn đáp án đúng:
Câu 4 :
Rút gọn biểu thức \(\left( {{9^{3 + \sqrt 3 }} - {9^{\sqrt 3 - 1}}} \right){.3^{ - 2\sqrt 3 }}\) được kết quả là:
Câu 5 :
Cho a, b là các số thực dương. Rút gọn biểu thức \(\frac{{{{\left( {\sqrt[4]{{{a^3}{b^2}}}} \right)}^8}}}{{\sqrt[3]{{\sqrt {{a^{12}}{b^6}} }}}}\)
Câu 6 :
Chọn đáp án đúng.
Câu 7 :
Chọn đáp án đúng. Cho a, b là các số thực dương. Giá trị của \(\ln \frac{a}{b} + \ln \frac{b}{a}\) bằng:
Câu 9 :
Cho \({\log _a}b = 4\). Giá trị của \({\log _a}\left( {{a^3}{b^2}} \right)\) bằng:
Câu 10 :
Cho hai số thực dương a, b thỏa mãn \({a^3}{b^2} = 1000\). Giá trị của biểu thức \(P = 3\log a + 2\log b\) là:
Câu 11 :
Trong các hàm số dưới đây, hàm số nào nghịch biến trên \(\left( {0; + \infty } \right)\)?
Câu 12 :
Hàm số nào dưới đây là hàm số đồng biến trên \(\mathbb{R}\)?
Câu 13 :
Đồ thị hàm số \(y = {6^{2x}}\) luôn đi qua điểm nào dưới đây?
Câu 15 :
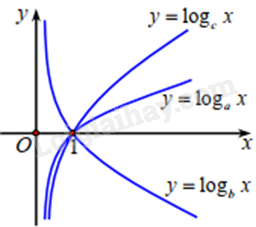
Cho ba số thực dương a, b, c khác 1. Đồ thị các hàm số \(y = {\log _a}x,y = {\log _b}x,y = {\log _c}x\) thể hiện ở hình vẽ dưới đây.
Khẳng định nào dưới đây là đúng?
Câu 16 :
Tập xác định của hàm số \(y = \frac{1}{{\sqrt {3 - x} }} + \ln \left( {x - 1} \right)\) là:
Câu 17 :
Bất phương trình \({6^x} \ge b\) có tập nghiệm là \(\mathbb{R}\) khi:
Câu 18 :
Tập nghiệm của bất phương trình \({\left( {\frac{1}{\pi }} \right)^x} > {\left( {\frac{1}{\pi }} \right)^3}\) là:
Câu 19 :
Tập nghiệm của bất phương trình \(\log x \ge 2\) là:
Câu 20 :
Cho phương trình \({4^x} + {2^{x + 2}} - 5 = 0\). Đặt \(t = {2^x}\) ta được phương trình là:
Câu 21 :
Phương trình \(\log _3^2x + 5{\log _3}x + 6 = 0\) có bao nhiêu nghiệm?
Câu 22 :
Bất phương trình \({\left( {\frac{1}{3}} \right)^{2{x^2} - 3x - 7}} - {3^{2x - 21}} > 0\) có nghiệm là:
Câu 23 :
Công thức \(M = {M_o}{\left( {\frac{1}{2}} \right)^{\frac{t}{T}}}\) cho biết khối lượng của một chất phóng xạ sau thời gian t kể từ thời điểm nào đó (gọi là thời điểm ban đầu), \({M_o}\) là khối lượng ban đầu, T là chu kì bán rã của chất phóng xạ đó (cứ sau mỗi chu kì, khối lượng của chất phóng xạ giảm đi một nửa). Trong một phòng thí nghiệm, với khối lượng 200g radon ban đầu, sau 16 ngày chỉ còn 11g. Chu kì bán rã của radon bằng (làm tròn kết quả đến hàng phần mười):
Câu 24 :
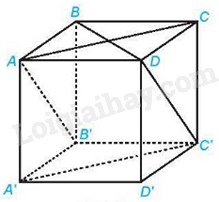
Cho hình hộp ABCD.A’B’C’D’ có các mặt là các hình vuông. Góc giữa hai đường thẳng AA’ và CD bằng:
Câu 25 :
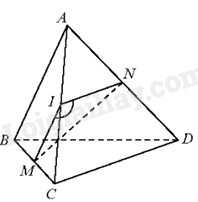
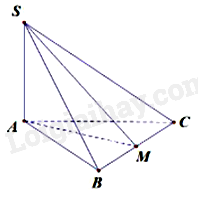
Cho tứ diện ABCD. Lấy điểm I bất kì thuộc cạnh AC. Qua I kẻ đường thẳng song song với AB cắt BC tại M. Qua I kẻ đường thẳng song song với CD cắt AD tại N. Khi đó, góc giữa hai đường thẳng AB và CD là:
Câu 26 :
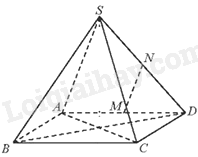
Cho hình chóp S. ABCD có ABCD là hình vuông cạnh bằng a và các cạnh bên đều bằng a. Gọi M, N lần lượt là trung điểm của AD, SD. Góc giữa hai đường thẳng MN và SC bằng:
Câu 27 :
Cho hình chóp S. ABCD với đáy ABCD có tất cả các cạnh bằng nhau. Gọi I, J lần lượt thuộc các cạnh SC, BC sao cho tam giác IJC là tam giác đều. Khi đó, góc giữa hai đường thẳng IJ và AD bằng:
Câu 28 :
Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\). Khẳng định nào sau đây là đúng?
Câu 29 :
Cho hình hộp ABCD.A’B’C’D’ có \(AA' \bot \left( {ABCD} \right)\). Khẳng định nào dưới đây đúng?
Câu 30 :
Trong không gian, cho điểm A và mặt phẳng (P). Mệnh nào dưới đây đúng?
Câu 31 :
Phát biểu nào sau đây là đúng?
Câu 32 :
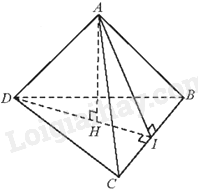
Cho tứ diện ABCD có ABC và BCD là các tam giác cân tại A và D. Gọi I là trung điểm của BC. Kẻ \(AH \bot DI\left( {H \in DI} \right)\). Hình chiếu vuông góc của A trên mặt phẳng (BCD) là:
Câu 33 :
Cho hình chóp S. ABC có \(SA \bot \left( {ABC} \right)\), M là trung điểm của BC. Tam giác ABC cân tại A. Mệnh đề nào sau đây sai?
Câu 34 :
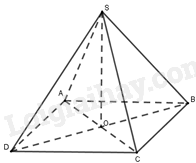
Cho hình chóp S. ABCD có đáy ABCD là hình thoi và \(SA = SC,{\rm{ }}SB = SD\). Gọi O là giao điểm của AC và BD. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) là:
Câu 35 :
Cho tứ diện ABCD có \(DA \bot \left( {ABC} \right)\), ABC là tam giác cân tại A. Gọi M là trung điểm của BC. Gọi G, K lần lượt là trọng tâm của tam giác ABC và DBC. Góc giữa hai đường thẳng GK và AB bằng:
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Câu 1 :
Khẳng định nào sau đây là đúng?
Đáp án : B Phương pháp giải :
Cho n là một số nguyên dương. Với a là số thực tùy ý khác 0, ta có \({a^{ - n}} = \frac{1}{{{a^n}}}\). Lời giải chi tiết :
\({4^{ - 6}} = \frac{1}{{{4^6}}}\) Đáp án B.
Câu 2 :
Chọn đáp án đúng. Cho số thực a và số nguyên dương n \(\left( {n \ge 2} \right)\). Số b được gọi là căn bậc n của số a nếu:
Đáp án : B Phương pháp giải :
Cho số thực a và số nguyên dương n \(\left( {n \ge 2} \right)\). Số b được gọi là căn bậc n của số a nếu \({b^n} = a\). Lời giải chi tiết :
Cho số thực a và số nguyên dương n \(\left( {n \ge 2} \right)\). Số b được gọi là căn bậc n của số a nếu \({b^n} = a\). Đáp án B.
Câu 3 :
Chọn đáp án đúng:
Đáp án : A Phương pháp giải :
\(\sqrt[n]{{{a^n}}} = a\) khi n lẻ (với các biểu thức đều có nghĩa). Lời giải chi tiết :
\(\sqrt[3]{{{{\left( {1 - \sqrt 5 } \right)}^3}}} = 1 - \sqrt 5 \). Đáp án A.
Câu 4 :
Rút gọn biểu thức \(\left( {{9^{3 + \sqrt 3 }} - {9^{\sqrt 3 - 1}}} \right){.3^{ - 2\sqrt 3 }}\) được kết quả là:
Đáp án : A Phương pháp giải :
Với a là số thực dương, \(\alpha ,\beta \) là những số thực bất kì thì: \({\left( {{a^\alpha }} \right)^\beta } = {a^{\alpha \beta }},{a^\alpha }.{a^\beta } = {a^{\alpha + \beta }}\). Cho n là một số nguyên dương. Với a là số thực tùy ý khác 0, ta có \({a^{ - n}} = \frac{1}{{{a^n}}}\). Lời giải chi tiết :
\(\left( {{9^{3 + \sqrt 3 }} - {9^{\sqrt 3 - 1}}} \right){.3^{ - 2\sqrt 3 }} = \left( {{3^{2\left( {3 + \sqrt 3 } \right)}} - {3^{2\left( {\sqrt 3 - 1} \right)}}} \right){.3^{ - 2\sqrt 3 }} = {3^{6 + 2\sqrt 3 - 2\sqrt 3 }} - {3^{2\sqrt 3 - 2 - 2\sqrt 3 }} = {3^6} - {3^{ - 2}} = {3^6} - \frac{1}{{{3^2}}} = \frac{{6560}}{9}\) Đáp án A.
Câu 5 :
Cho a, b là các số thực dương. Rút gọn biểu thức \(\frac{{{{\left( {\sqrt[4]{{{a^3}{b^2}}}} \right)}^8}}}{{\sqrt[3]{{\sqrt {{a^{12}}{b^6}} }}}}\)
Đáp án : D Phương pháp giải :
\(\sqrt[n]{{{a^n}}} = \left| a \right|\) nếu n là số chẵn. \(\sqrt[m]{{\sqrt[n]{a}}} = \sqrt[{mn}]{a}\) (các biểu thức đều có nghĩa) Lời giải chi tiết :
\(\frac{{{{\left( {\sqrt[4]{{{a^3}{b^2}}}} \right)}^8}}}{{\sqrt[3]{{\sqrt {{a^{12}}{b^6}} }}}} = \frac{{{{\left( {{{\left( {\sqrt[4]{{{a^3}{b^2}}}} \right)}^4}} \right)}^2}}}{{\sqrt[6]{{{{\left( {{a^2}b} \right)}^6}}}}} = \frac{{{{\left( {{a^3}{b^2}} \right)}^2}}}{{{a^2}b}} = \frac{{{a^6}{b^4}}}{{{a^2}b}} = {a^4}{b^3}\) Đáp án D.
Câu 6 :
Chọn đáp án đúng.
Đáp án : A Phương pháp giải :
Với số thực dương a, b và \(a \ne 1\) thì: + \({\log _a}{a^b} = b\) + \({\log _e}b\) được viết là ln b Lời giải chi tiết :
\(\ln {e^2} = 2\) Đáp án A.
Câu 7 :
Chọn đáp án đúng. Cho a, b là các số thực dương. Giá trị của \(\ln \frac{a}{b} + \ln \frac{b}{a}\) bằng:
Đáp án : D Phương pháp giải :
Với số thực dương a, b, c và \(a \ne 1\) thì: + \({\log _e}b\) được viết là ln b. + \({\log _a}1 = 0\), \({\log _a}\left( {bc} \right) = {\log _a}b + {\log _a}c\). Lời giải chi tiết :
\(\ln \frac{a}{b} + \ln \frac{b}{a} = \ln \left( {\frac{a}{b}.\frac{b}{a}} \right) = \ln 1 = 0\) Đáp án D.
Đáp án : B Phương pháp giải :
Cho \(a > 0,a \ne 1,b > 0\). Với mọi số nguyên dương \(n \ge 2\) ta có \({\log _a}\sqrt[n]{b} = \frac{1}{n}{\log _a}b\). Lời giải chi tiết :
Cho \(a > 0,a \ne 1,b > 0\). Với mọi số nguyên dương \(n \ge 2\) ta có \({\log _a}\sqrt[n]{b} = \frac{1}{n}{\log _a}b\). Đáp án B.
Câu 9 :
Cho \({\log _a}b = 4\). Giá trị của \({\log _a}\left( {{a^3}{b^2}} \right)\) bằng:
Đáp án : D Phương pháp giải :
+ Với a, b là số thực dương và \(a \ne 1\) thì \(\log {\,_a}{a^\alpha } = \alpha ,\log {\,_a}{b^\alpha } = \alpha \log {\,_a}b\) + Với \(0 < a \ne 1,b,c > 0\) thì \({\log _a}\left( {bc} \right) = {\log _a}b + {\log _a}c\). Lời giải chi tiết :
\({\log _a}\left( {{a^3}{b^2}} \right) = {\log _a}{a^3} + {\log _a}{b^2} = 3 + 2{\log _a}b = 3 + 2.4 = 11\) Đáp án D.
Câu 10 :
Cho hai số thực dương a, b thỏa mãn \({a^3}{b^2} = 1000\). Giá trị của biểu thức \(P = 3\log a + 2\log b\) là:
Đáp án : C Phương pháp giải :
+ Với a, b là số thực dương và \(a \ne 1\) thì \(\log {\,_a}{a^\alpha } = \alpha ,\log {\,_a}{b^\alpha } = \alpha \log {\,_a}b\). + Với \(0 < a \ne 1,b,c > 0\) thì \({\log _a}\left( {bc} \right) = {\log _a}b + {\log _a}c\). Lời giải chi tiết :
\(P = 3\log a + 2\log b = \log {a^3} + \log {b^2} = \log \left( {{a^3}{b^2}} \right) = \log 1000 = \log {10^3} = 3\) Đáp án C.
Câu 11 :
Trong các hàm số dưới đây, hàm số nào nghịch biến trên \(\left( {0; + \infty } \right)\)?
Đáp án : B Phương pháp giải :
Với \(0 < a < 1\) thì hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) nghịch biến trên \(\left( {0; + \infty } \right)\). Lời giải chi tiết :
Vì \(0 < \frac{1}{\pi } < 1\) nên hàm số \(y = {\log _{\frac{1}{\pi }}}x\) nghịch biến trên \(\left( {0; + \infty } \right)\). Đáp án B.
Câu 12 :
Hàm số nào dưới đây là hàm số đồng biến trên \(\mathbb{R}\)?
Đáp án : A Phương pháp giải :
Với \(a > 1\) thì hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) đồng biến trên \(\mathbb{R}\). Lời giải chi tiết :
Vì \(3 > 1\) nên hàm số \(y = {3^x}\) đồng biến trên \(\mathbb{R}\). Đáp án A.
Câu 13 :
Đồ thị hàm số \(y = {6^{2x}}\) luôn đi qua điểm nào dưới đây?
Đáp án : A Phương pháp giải :
Đồ thị hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) luôn đi qua điểm (0; 1). Lời giải chi tiết :
Đồ thị hàm số \(y = {6^{2x}}\) luôn đi qua điểm (0; 1). Đáp án A.
Đáp án : B Phương pháp giải :
Hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) được gọi là hàm số lôgarit cơ số a. Lời giải chi tiết :
Hàm số \(y = \log x\) có cơ số là 10. Đáp án B.
Câu 15 :
Cho ba số thực dương a, b, c khác 1. Đồ thị các hàm số \(y = {\log _a}x,y = {\log _b}x,y = {\log _c}x\) thể hiện ở hình vẽ dưới đây.
Khẳng định nào dưới đây là đúng?
Đáp án : A Phương pháp giải :
Nếu \(0 < a < 1\) thì hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) nghịch biến trên \(\left( {0; + \infty } \right)\). Nếu \(a > 1\) thì hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) đồng biến trên \(\left( {0; + \infty } \right)\). Lời giải chi tiết :
Ta thấy hàm số \(y = {\log _b}x\) nghịch biến trên \(\left( {0; + \infty } \right)\) nên \(b < 1\). Hàm số \(y = {\log _a}x,y = {\log _c}x\) đồng biến trên \(\left( {0; + \infty } \right)\) nên \(a > 1,c > 1\). Xét tại một điểm \(x > 1\) thì: \({\log _c}x > {\log _a}x \Rightarrow {\log _c}x > \frac{1}{{{{\log }_x}a}} \Rightarrow {\log _c}x.{\log _x}a > 1 \Rightarrow a > c\) Do đó, \(b < c < a\). Đáp án A.
Câu 16 :
Tập xác định của hàm số \(y = \frac{1}{{\sqrt {3 - x} }} + \ln \left( {x - 1} \right)\) là:
Đáp án : C Phương pháp giải :
Hàm số \(y = \ln u\left( x \right)\) xác định khi \(u\left( x \right) > 0\). Hàm số \(y = \frac{1}{{\sqrt {u\left( x \right)} }}\) xác định khi \(u\left( x \right) > 0\). Lời giải chi tiết :
Hàm số \(y = \frac{1}{{\sqrt {3 - x} }} + \ln \left( {x - 1} \right)\) xác định khi \(\left\{ \begin{array}{l}3 - x > 0\\x - 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x < 3\\x > 1\end{array} \right.\) Vậy tập xác định của hàm số là: \(D = \left( {1;3} \right)\). Đáp án C.
Câu 17 :
Bất phương trình \({6^x} \ge b\) có tập nghiệm là \(\mathbb{R}\) khi:
Đáp án : C Phương pháp giải :
Bất phương trình \({a^x} \ge b\left( {0 < a \ne 1} \right)\) có tập nghiệm là \(\mathbb{R}\) khi \(b \le 0\). Lời giải chi tiết :
Bất phương trình \({6^x} \ge b\) có tập nghiệm là \(\mathbb{R}\) khi \(b \le 0\). Đáp án C.
Câu 18 :
Tập nghiệm của bất phương trình \({\left( {\frac{1}{\pi }} \right)^x} > {\left( {\frac{1}{\pi }} \right)^3}\) là:
Đáp án : D Phương pháp giải :
Với \(0 < a < 1\) thì \({a^{u\left( x \right)}} > {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) < v\left( x \right)\). Lời giải chi tiết :
\({\left( {\frac{1}{\pi }} \right)^x} > {\left( {\frac{1}{\pi }} \right)^3} \Leftrightarrow x < 3\) Vậy tập nghiệm của bất phương trình là: \(S = \left( { - \infty ;3} \right)\) Đáp án D.
Câu 19 :
Tập nghiệm của bất phương trình \(\log x \ge 2\) là:
Đáp án : B Phương pháp giải :
Bất phương trình \({\log _a}x \ge b\left( {a > 1} \right) \Leftrightarrow x \ge {a^b}\). Lời giải chi tiết :
\(\log x \ge 2 \Leftrightarrow x \ge {10^2} \Leftrightarrow x \ge 100\) (thỏa mãn) Vậy bất phương trình có tập nghiệm là \(S = \left[ {100; + \infty } \right)\). Đáp án B.
Câu 20 :
Cho phương trình \({4^x} + {2^{x + 2}} - 5 = 0\). Đặt \(t = {2^x}\) ta được phương trình là:
Đáp án : C Phương pháp giải :
Phương trình hàm số mũ. Cho a, b là số thực dương và \(\alpha ,\beta \) là những số thực bất kì. Khi đó, \({\left( {{a^\alpha }} \right)^\beta } = {a^{\alpha .\beta }},{a^\alpha }.{a^\beta } = {a^{\alpha + \beta }}\) Lời giải chi tiết :
\({4^x} + {2^{x + 2}} - 5 = 0 \Leftrightarrow {\left( {{2^x}} \right)^2} + {4.2^x} - 5 = 0\;\;\left( 1 \right)\) Đặt \(t = {2^x}\) thì phương trình trở thành: \({t^2} + 4t - 5 = 0\). Đáp án C.
Câu 21 :
Phương trình \(\log _3^2x + 5{\log _3}x + 6 = 0\) có bao nhiêu nghiệm?
Đáp án : C Phương pháp giải :
Với \(a > 0,a \ne 1\) ta có: \({\log _a}u\left( x \right) = b \Leftrightarrow u\left( x \right) = {a^b}\). Lời giải chi tiết :
Điều kiện: \(x \ge 0\) Đặt \({\log _3}x = t\) thì phương trình \(\log _3^2x + 5{\log _3}x + 6 = 0\) trở thành: \({t^2} + 5t + 6 = 0 \Leftrightarrow \left( {t + 2} \right)\left( {t + 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}t = - 2\\t = - 3\end{array} \right.\) Với \(t = - 2\) thì \({\log _3}x = - 2 \Leftrightarrow x = {3^{ - 2}} = \frac{1}{9}\) (thỏa mãn) Với \(t = - 3\) thì \({\log _3}x = - 3 \Leftrightarrow x = {3^{ - 3}} = \frac{1}{{27}}\) (thỏa mãn) Vậy phương trình đã cho có 2 nghiệm. Đáp án C.
Câu 22 :
Bất phương trình \({\left( {\frac{1}{3}} \right)^{2{x^2} - 3x - 7}} - {3^{2x - 21}} > 0\) có nghiệm là:
Đáp án : D Phương pháp giải :
Nếu \(a > 1\) thì \({a^{u\left( x \right)}} > {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) > v\left( x \right)\) Lời giải chi tiết :
\({\left( {\frac{1}{3}} \right)^{2{x^2} - 3x - 7}} - {3^{2x - 21}} > 0 \Leftrightarrow {3^{ - \left( {2{x^2} - 3x - 7} \right)}} > {3^{2x - 21}} \Leftrightarrow - 2{x^2} + 3x + 7 > 2x - 21 \Leftrightarrow 2{x^2} - x - 28 < 0\) \( \Leftrightarrow \left( {2x + 7} \right)\left( {x - 4} \right) < 0 \Leftrightarrow \frac{{ - 7}}{2} < x < 4\) Đáp án D.
Câu 23 :
Công thức \(M = {M_o}{\left( {\frac{1}{2}} \right)^{\frac{t}{T}}}\) cho biết khối lượng của một chất phóng xạ sau thời gian t kể từ thời điểm nào đó (gọi là thời điểm ban đầu), \({M_o}\) là khối lượng ban đầu, T là chu kì bán rã của chất phóng xạ đó (cứ sau mỗi chu kì, khối lượng của chất phóng xạ giảm đi một nửa). Trong một phòng thí nghiệm, với khối lượng 200g radon ban đầu, sau 16 ngày chỉ còn 11g. Chu kì bán rã của radon bằng (làm tròn kết quả đến hàng phần mười):
Đáp án : A Phương pháp giải :
Phương trình \({a^x} = b\left( {a > 0,a \ne 1} \right)\) với \(b > 0\) có nghiệm là \(x = {\log _a}b\) Lời giải chi tiết :
Với \({M_o} = 200g,t = 16,M = 11g\) thay vào công thức \(M = {M_o}{\left( {\frac{1}{2}} \right)^{\frac{t}{T}}}\) ta có: \(11 = 200{\left( {\frac{1}{2}} \right)^{\frac{{16}}{T}}} \Leftrightarrow \frac{{16}}{T} = {\log _{\frac{1}{2}}}\frac{{11}}{{200}} = {\log _2}\frac{{200}}{{11}} \Leftrightarrow T = \frac{{16}}{{{{\log }_2}\frac{{200}}{{11}}}} \approx 3,8\) (ngày) Đáp án A.
Câu 24 :
Cho hình hộp ABCD.A’B’C’D’ có các mặt là các hình vuông. Góc giữa hai đường thẳng AA’ và CD bằng:
Đáp án : A Phương pháp giải :
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b; kí hiệu \(\left( {a,b} \right)\) hoặc \(\widehat {\left( {a;b} \right)}\). Lời giải chi tiết :
Vì AB//CD nên \(\left( {AA',CD} \right) = \left( {AA',AB} \right) = {90^0}\) Đáp án A.
Câu 25 :
Cho tứ diện ABCD. Lấy điểm I bất kì thuộc cạnh AC. Qua I kẻ đường thẳng song song với AB cắt BC tại M. Qua I kẻ đường thẳng song song với CD cắt AD tại N. Khi đó, góc giữa hai đường thẳng AB và CD là:
Đáp án : C Phương pháp giải :
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b; kí hiệu \(\left( {a,b} \right)\) hoặc \(\widehat {\left( {a;b} \right)}\). Lời giải chi tiết :
Vì MI//AB, IN//CD nên \(\left( {AB,CD} \right) = \left( {IM,IN} \right)\). Đáp án C.
Câu 26 :
Cho hình chóp S. ABCD có ABCD là hình vuông cạnh bằng a và các cạnh bên đều bằng a. Gọi M, N lần lượt là trung điểm của AD, SD. Góc giữa hai đường thẳng MN và SC bằng:
Đáp án : A Phương pháp giải :
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b; kí hiệu \(\left( {a,b} \right)\) hoặc \(\widehat {\left( {a;b} \right)}\). Lời giải chi tiết :
Vì M, N lần lượt là trung điểm của AD, SD nên MN là đường trung bình của tam giác SAD. Do đó, MN//AS. Suy ra, \(\left( {MN,SC} \right) = \left( {SA,SC} \right) = \widehat {SAC}\). Vì tam giác ABC vuông tại B nên \(A{C^2} = A{B^2} + B{C^2} = 2{a^2}\) Vì \(A{C^2} = S{A^2} + A{C^2}\) nên tam giác SAC vuông tại S (định lí Pythagore đảo) Do đó, \(\widehat {ASC} = {90^0}\). Vậy \(\left( {MN,SC} \right) = {90^0}\). Đáp án A.
Câu 27 :
Cho hình chóp S. ABCD với đáy ABCD có tất cả các cạnh bằng nhau. Gọi I, J lần lượt thuộc các cạnh SC, BC sao cho tam giác IJC là tam giác đều. Khi đó, góc giữa hai đường thẳng IJ và AD bằng:
Đáp án : A Phương pháp giải :
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b; kí hiệu \(\left( {a,b} \right)\) hoặc \(\widehat {\left( {a;b} \right)}\). Lời giải chi tiết :
Tứ giác ABCD có: \(AB = BC = CD = DA\) nên tứ giác ABCD là hình thoi. Do đó, AD//BC. Suy ra: \(\left( {IJ,AD} \right) = \left( {IJ,BC} \right) = \widehat {CJI}\) Tam giác IJC là tam giác đều nên \(\widehat {IJC} = {60^0}\). Do đó, góc giữa hai đường thẳng IJ và AD bằng \({60^0}\). Đáp án A.
Câu 28 :
Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\). Khẳng định nào sau đây là đúng?
Đáp án : A Phương pháp giải :
Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó. Lời giải chi tiết :
Vì \(SA \bot \left( {ABC} \right)\) và \(AB,BC,CA \subset \left( {ABC} \right)\) nên \(SA \bot BC\), \(SA \bot AC\), \(SA \bot AB\). Đáp án D.
Câu 29 :
Cho hình hộp ABCD.A’B’C’D’ có \(AA' \bot \left( {ABCD} \right)\). Khẳng định nào dưới đây đúng?
Đáp án : B Phương pháp giải :
Cho hai đường thẳng song song, mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia. Lời giải chi tiết :
Vì \(AA' \bot \left( {ABCD} \right)\) và AA’//BB’ nên \(BB' \bot \left( {ABCD} \right)\) Đáp án B.
Câu 30 :
Trong không gian, cho điểm A và mặt phẳng (P). Mệnh nào dưới đây đúng?
Đáp án : B Phương pháp giải :
Có đúng một đường thẳng đi qua A và vuông góc với (P). Lời giải chi tiết :
Có đúng một đường thẳng đi qua A và vuông góc với (P). Đáp án B.
Câu 31 :
Phát biểu nào sau đây là đúng?
Đáp án : D Phương pháp giải :
Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau trong mặt phẳng (P) thì d vuông góc với (P). Lời giải chi tiết :
Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau trong mặt phẳng (P) thì d vuông góc với (P). Đáp án D.
Câu 32 :
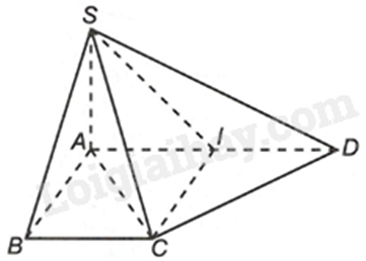
Cho tứ diện ABCD có ABC và BCD là các tam giác cân tại A và D. Gọi I là trung điểm của BC. Kẻ \(AH \bot DI\left( {H \in DI} \right)\). Hình chiếu vuông góc của A trên mặt phẳng (BCD) là:
Đáp án : B Phương pháp giải :
+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\). + Cho mặt phẳng (P). Xét một điểm M tùy ý trong không gian. Gọi d là đường thẳng đi qua điểm M và vuông góc với (P). Gọi M’ là giao điểm của đường thẳng d và mặt phẳng (P). Khi đó, điểm M’ được gọi là hình chiếu vuông góc của điểm M lên mặt phẳng (P). Lời giải chi tiết :
Vì tam giác ABC cân tại A nên AI là đường trung tuyến đồng thời là đường cao. Do đó, \(AI \bot BC\). Vì tam giác DBC cân tại D nên DI là đường trung tuyến đồng thời là đường cao. Do đó, \(DI \bot BC\). Ta có: \(AI \bot BC\), \(DI \bot BC\), DI và AI cắt nhau tại I và nằm trong mặt phẳng (AID) nên \(BC \bot \left( {AID} \right)\). Mà \(AH \subset \left( {ADI} \right) \Rightarrow AH \bot CB\) Lại có: \(AH \bot DI\), DI và BC cắt nhau tại I và nằm trong mặt phẳng (BCD). Do đó, \(AH \bot \left( {BCD} \right)\). Do đó, hình chiếu vuông góc của A trên mặt phẳng (BCD) là điểm H. Đáp án B.
Câu 33 :
Cho hình chóp S. ABC có \(SA \bot \left( {ABC} \right)\), M là trung điểm của BC. Tam giác ABC cân tại A. Mệnh đề nào sau đây sai?
Đáp án : A Phương pháp giải :
Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\). Lời giải chi tiết :
Vì \(SA \bot \left( {ABC} \right),BC \subset \left( {ABC} \right) \Rightarrow SA \bot BC\) Tam giác ABC cân tại A nên AM là đường trung tuyến đồng thời là đường cao. Do đó, \(BC \bot AM\) Vì \(SA \bot BC\), \(BC \bot AM\), SA và AM cắt nhau tại A và nằm trong mặt phẳng (SAM) nên \(BC \bot \left( {SAM} \right)\), mà \(SM \subset \left( {SAM} \right)\)\( \Rightarrow BC \bot SM\) Tam giác SBC có \(BC \bot SM\) nên BC không thể vuông góc với SB. Do đó, câu A sai. Đáp án A.
Câu 34 :
Cho hình chóp S. ABCD có đáy ABCD là hình thoi và \(SA = SC,{\rm{ }}SB = SD\). Gọi O là giao điểm của AC và BD. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) là:
Đáp án : C Phương pháp giải :
+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\). + Cho mặt phẳng (P). Xét một điểm M tùy ý trong không gian. Gọi d là đường thẳng đi qua điểm M và vuông góc với (P). Gọi M’ là giao điểm của đường thẳng d và mặt phẳng (P). Khi đó, điểm M’ được gọi là hình chiếu vuông góc của điểm M lên mặt phẳng (P). Lời giải chi tiết :
Vì ABCD là hình thoi, O là giao điểm của AC và BD nên O là trung điểm của AC, O là trung điểm của BD. Vì \(SA = SC\) nên tam giác SAC cân tại S. Do đó, SO là đường trung tuyến đồng thời là đường cao của tam giác. Suy ra, \(SO \bot AC\). Vì \(SB = SD\) nên tam giác SBD cân tại S. Do đó, SO là đường trung tuyến đồng thời là đường cao của tam giác. Suy ra, \(SO \bot BD\). Vì \(SO \bot AC\), \(SO \bot BD\) và BD và AC cắt nhau tại O và nằm trong mặt phẳng (ABCD) nên \(SO \bot \left( {ABCD} \right)\). Do đó, hình chiếu vuông góc của S lên mặt phẳng (ABCD) là điểm O. Đáp án C.
Câu 35 :
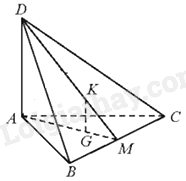
Cho tứ diện ABCD có \(DA \bot \left( {ABC} \right)\), ABC là tam giác cân tại A. Gọi M là trung điểm của BC. Gọi G, K lần lượt là trọng tâm của tam giác ABC và DBC. Góc giữa hai đường thẳng GK và AB bằng:
Đáp án : C Phương pháp giải :
Cho hai đường thẳng song song, mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia. Lời giải chi tiết :
Vì K là trọng tâm của tam giác DBC, DM là đường trung tuyến của tam giác DBC nên \(\frac{{MK}}{{MD}} = \frac{1}{3}\) Vì G là trọng tâm của tam giác ABC, AM là đường trung tuyến của tam giác ABC nên \(\frac{{MG}}{{MA}} = \frac{1}{3}\) Tam giác DMA có: \(\frac{{MK}}{{MD}} = \frac{{MG}}{{MA}}\left( { = \frac{1}{3}} \right)\) nên GK//AD Mà \(AD \bot \left( {ABC} \right)\) suy ra \(GK \bot \left( {ABC} \right)\). Mà \(AB \subset \left( {ABC} \right) \Rightarrow GK \bot AB\) Do đó, góc giữa hai đường thẳng GK và AB bằng \({90^0}\). Đáp án C.
II. Tự luận
Phương pháp giải :
Hàm số \(y = \log u\left( x \right)\) xác định khi \(u\left( x \right) > 0\). Lời giải chi tiết :
a) Với \(m = 3\) ta có: \(y = \log \left( {{x^2} + 8x + 6} \right)\). Hàm số \(y = \log \left( {{x^2} + 8x + 6} \right)\) xác định khi \({x^2} + 8x + 6 > 0 \Leftrightarrow \left[ \begin{array}{l}x > - 4 + \sqrt {10} \\x < - 4 - \sqrt {10} \end{array} \right.\) Vậy với \(m = 3\) thì tập xác định của hàm số là: \(D = \left( { - \infty ; - 4 - \sqrt {10} } \right) \cup \left( { - 4 + \sqrt {10} ; + \infty } \right)\). b) Hàm số \(y = \log \left[ {\left( {m - 2} \right){x^2} + 2\left( {m + 1} \right)x + 2m} \right]\) xác định với mọi giá trị thực của x khi và chỉ khi \(f\left( x \right) = \left( {m - 2} \right){x^2} + 2\left( {m + 1} \right)x + 2m > 0\) với mọi \(x \in \mathbb{R}\) Trường hợp 1: Với \(m = 2\) ta có: \(f\left( x \right) = 6x + 4 > 0 \Leftrightarrow x > \frac{{ - 2}}{3}\). Do đó, f(x) không xác định với mọi giá trị thực của x. Do đó, \(m = 2\) không thỏa mãn. Trường hợp 2: Với \(m \ne 2\). Hàm số \(f\left( x \right) = \left( {m - 2} \right){x^2} + 2\left( {m + 1} \right)x + 2m > 0\) với mọi \(x \in \mathbb{R}\) \( \Leftrightarrow \left\{ \begin{array}{l}m - 2 > 0\\\Delta ' = {\left( {m + 1} \right)^2} - \left( {m - 2} \right)2m < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 2\\ - {m^2} + 6m + 1 < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 2\\\left[ \begin{array}{l}m < 3 - \sqrt {10} \\m > 3 + \sqrt {10} \end{array} \right.\end{array} \right. \Leftrightarrow m > 3 + \sqrt {10} \) Vậy với \(m \in \left( {3 + \sqrt {10} ; + \infty } \right)\) thì hàm số \(y = \log \left[ {\left( {m - 2} \right){x^2} + 2\left( {m + 1} \right)x + 2m} \right]\) có tập xác định với mọi giá trị thực của x. Phương pháp giải :
+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\). + Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó. Lời giải chi tiết :
a) Vì \(SA \bot \left( {ABCD} \right),BC \subset \left( {ABCD} \right) \Rightarrow SA \bot BC\). Vì ABCD là hình thang vuông tại A và B nên \(AB \bot BC\). Ta có: \(SA \bot BC\), \(AB \bot BC\), SA và AB cắt nhau tại A và nằm trong mặt phẳng (SAB) nên \(BC \bot \left( {SAB} \right)\). Lại có, \(SB \subset \left( {SBC} \right) \Rightarrow BC \bot SB\). Suy ra, tam giác SBC vuông tại B. b) Gọi I là trung điểm của AD. Do đó, \(AI = ID = \frac{1}{2}AD = a\) Tứ giác ABCI có: AI//BC (do tứ giác ABCD là hình thang vuông tại A, B), \(AI = BC\left( { = a} \right)\) nên tứ giác ABCI là hình bình hành. Lại có: \(BC = AB\) nên tứ giác ABCI là hình thoi. Mà \(\widehat {BAI} = {90^0}\) nên ABCI là hình vuông. Do đó, \(\widehat {AIC} = {90^0} \Rightarrow \widehat {CID} = {90^0}\) Tam giác CID có: \(\widehat {CID} = {90^0},CI = ID\left( { = a} \right)\) nên tam giác CID vuông cân tại I. Suy ra: \(\widehat {DCI} = {45^0}\). Lại có: CA là phân giác góc ICB (do ABCI là hình vuông) nên \(\widehat {ACI} = \frac{1}{2}\widehat {ICB} = \frac{1}{2}{.90^0} = {45^0}\) Suy ra: \(\widehat {ACD} = \widehat {ACI} + \widehat {ICD} = {90^0}\) hay \(AC \bot CD\) Vì \(SA \bot \left( {ABCD} \right),DC \subset \left( {ABCD} \right) \Rightarrow SA \bot DC\) Ta có: \(AC \bot CD\), \(SA \bot DC\), SA và AC cắt nhau tại A và nằm trong mặt phẳng (SAC) nên \(DC \bot \left( {SAC} \right)\). Mà \(SC \subset \left( {SAC} \right) \Rightarrow CD \bot SC\) Phương pháp giải :
+ Nếu \(a > 0,a \ne 1\) thì \({\log _a}u\left( x \right) = {\log _a}v\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}u\left( x \right) > 0\\u\left( x \right) = v\left( x \right)\end{array} \right.\) (có thể thay \(u\left( x \right) > 0\) bằng \(v\left( x \right) > 0\)) + Với \(a > 0,a \ne 1\) ta có: \({\log _a}u\left( x \right) = b \Leftrightarrow u\left( x \right) = {a^b}\). Lời giải chi tiết :
Điều kiện: \({\log _3}{x^5} \ge m > 0,x > 0\) \(\left( {{4^x} - {{10.2}^x} + 16} \right)\sqrt {{{\log }_3}{x^5} - m} = 0 \Leftrightarrow \left[ \begin{array}{l}{4^x} - {10.2^x} + 16 = 0\;\left( 1 \right)\\{\log _3}{x^5} - m = 0\;\;\left( 2 \right)\end{array} \right.\) Giải phương trình (1): \({\left( {{2^x}} \right)^2} - {10.2^x} + 16 = 0 \Leftrightarrow \left( {{2^x} - 2} \right)\left( {{2^x} - 8} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{2^x} - 2 = 0\\{2^x} - 8 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 3\end{array} \right.\) (thỏa mãn) Vì \(m \in \mathbb{N}*\) nên phương trình (2) luôn có nghiệm \(x = \sqrt[5]{{{3^m}}}\). Để phương trình có đúng hai nghiệm phân biệt thì: + Trường hợp 1: \(x = \sqrt[5]{{{3^m}}} = 1 \Rightarrow m = 0\) (loại) + Trường hợp 2: \(x = \sqrt[5]{{{3^m}}} = 2 \Rightarrow {3^{\frac{m}{5}}} = 2 \Rightarrow m = 5{\log _3}2\) (loại) + Trường hợp 3: Phương trình đã cho chỉ nhận nghiệm \(x = 3\) của phương trình (1) làm nghiệm, một nghiệm từ (2): Khi đó, \(\left\{ \begin{array}{l}m = 5{\log _3}x,x < 3\\5{\log _3}1 < m\end{array} \right. \Rightarrow \left\{ \begin{array}{l}0 < m < 5\\x = \sqrt[5]{{{3^m}}}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}m \in \left\{ {1;2;3;4} \right\}\\x = \sqrt[5]{{{3^m}}}\end{array} \right.\) Suy ra, với \(m \in \left\{ {1;2;3;4} \right\}\) thì phương trình đã cho có hai nghiệm \(x = \sqrt[5]{{{3^m}}}\), \(x = 3\). Vậy \(m \in \left\{ {1;2;3;4} \right\}\) phương trình đã cho có đúng hai nghiệm phân biệt.
|