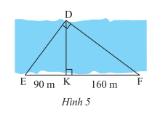
Giải bài 13 trang 86 SGK Toán 8 tập 2– Chân trời sáng tạo

Đề bài

Người ta đo khoảng cách giữa hai điểm $D$ và $K$ ở hai bờ một dòng song (Hình 5). Cho biết $KE = 90m,KF = 160m$. Tính khoảng cách $DK$.

 

Lời giải chi tiết

- Xét tam giác $DEF$ và tam giác $KDF$ có:

$\widehat F$ (chung)

$\widehat {EDF} = \widehat {DKF} = 90^\circ$ (giải thuyết)

Suy ra, $\Delta DEF\backsim\Delta KDF$ (g.g)

Suy ra, $\widehat E = \widehat {KDF}$ (hai góc tương ứng).

- Xét tam giác $DEK$ và tam giác $FDK$ có:

$\widehat E = \widehat {KDF}$ (chứng minh trên)

$\widehat {EKD} = \widehat {FKD} = 90^\circ$ (giải thuyết)

Suy ra, $\Delta DEK\backsim\Delta FDK$ (g.g)

Suy ra, $\frac{{DK}}{{FK}} = \frac{{EK}}{{DK}}$ (các cặp cạnh tương ứng có cùng tỉ lệ)

Suy ra, $D{K^2} = EK.FK = 90.160 = 14400 \Rightarrow DK = \sqrt {14400}  = 120$.

Vậy khoảng cách $DK = 120m$.