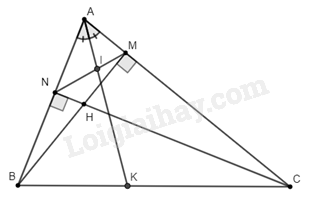
Giải bài 15 trang 86 SGK Toán 8 tập 2– Chân trời sáng tạo

Đề bài

Cho tam giác $ABC$ nhọn có hai đường cao $BM,CN$ cắt nhau tại $H$.

a) Chứng minh rằng $\Delta AMN\backsim\Delta ABC$.

b) Phân giác của $\widehat {BAC}$ cắt $MN$ và $BC$ lần lượt tại $I$ và $K$. Chứng minh rằng $\frac{{IM}}{{IN}} = \frac{{KB}}{{KC}}$.

Lời giải chi tiết

a) Vì $BM$ là đường cao nên $\widehat {AMB} = 90^\circ$; vì $CN$ là đường cao nên $\widehat {ANC} = 90^\circ$

Xét tam giác $AMB$ và tam giác $ANC$ có:

$\widehat A$ (chung)

$\widehat {ANB} = \widehat {ANC} = 90^\circ$ (chứng minh trên)

Suy ra, $\Delta AMB\backsim\Delta ANC$ (g.g).

Suy ra, $\frac{{AM}}{{AN}} = \frac{{AB}}{{AC}}$ (các cặp cạnh tương ứng có cùng tỉ lệ).

Do đó, $\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}$ (tỉ lệ thức)

Xét tam giác $AMN$ và tam giác $ABC$ có:

$\widehat A$ (chung)

$\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}$ (chứng minh trên)

Suy ra, $\Delta AMN\backsim\Delta ABC$ (c.g.c).

b) Xét tam giác $AMN$ có $AI$ là đường phân giác của $\widehat {MAN}\left( {I \in MN} \right)$.

Theo tính chất đường phân giác ta có:

$\frac{{IM}}{{IN}} = \frac{{AM}}{{AN}}$

Xét tam giác $ABC$ có $AK$ là đường phân giác của $\widehat {BAC}\left( {K \in BC} \right)$.

Theo tính chất đường phân giác ta có:

$\frac{{BK}}{{KC}} = \frac{{AB}}{{AC}}$

Mà $\frac{{AM}}{{AN}} = \frac{{AB}}{{AC}}$ (chứng minh trên) nên $\frac{{IM}}{{IN}} = \frac{{KB}}{{KC}}$ (điều phải chứng minh).