Giải bài 2.28 trang 27 sách bài tập toán 10 - Kết nối tri thức với cuộc sốngHỏi số tiền lãi lớn nhất mà phân xưởng này có thể thu được trong một ngày là bao nhiêu? Đề bài Một phân xưởng có hai loại máy chuyên dụng \({M_1}\) và \({M_2}\) để sản xuất hai loại sản phẩm A và B theo đơn đặt hàng. Nếu sản xuất được một tấn sản phẩm loại A thì phân xưởng nhận được số tiền lãi là 2 triệu đồng. Nếu sản xuất được một tấn sản phẩm loại B thì phân xưởng nhận được số tiền lãi là 1,6 triệu đồng. Muốn sản xuất một tấn sản phẩm loại A, người ta phải dùng máy \({M_1}\) trong 3 giờ và máy \({M_2}\) trong 1 giờ. Muốn sản xuất một tấn sản phẩm loại B, người ta phải dùng máy \({M_1}\) trong 1 giờ và máy \({M_2}\) trong 1 giờ. Một máy không thể dùng sản xuất đồng thời hai loại sản phẩm. Máy \({M_1}\) làm việc không quá 6 giờ một ngày và máy \({M_2}\) làm việc không quá 4 giờ một ngày. Hỏi số tiền lãi lớn nhất mà phân xưởng này có thể thu được trong một ngày là bao nhiêu? Phương pháp giải - Xem chi tiết - Viết hệ bất phương trình của bài toán nói trên - Xác định miền nghiệm của hệ bất phương trình - Viết biểu thức biểu thị số tiền lại phân xưởng thu được đạt giá trị lớn nhất Lời giải chi tiết
Điều kiện: \(x \ge 0;\,\,y \ge 0.\) Thời gian máy \({M_1}\) làm việc không quá 6 giờ một ngày là: \(3x + y \le 6.\) Thời gian máy \({M_2}\) làm việc không quá 4 giờ một ngày là: \(x + y \le 4.\) Ta có hệ bất phương trình: \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{3x + y \le 6}\\{x + y \le 4}\end{array}.} \right.\) Số tiền lãi phân xưởng này thu được trong một ngày là: \(F\left( {x;y} \right) = 2x + 1,6y \to \max \)
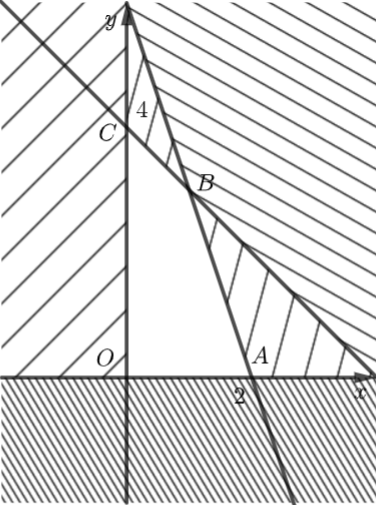
Miền nghiệm của bất phương trình \(d:x \ge 0\) là nửa mặt phẳng bờ \(d\) chứa điểm \(\left( {1;0} \right).\) Miền nghiệm của bất phương trình \({d_1}:y \ge 0\) là nửa mặt phẳng bờ \({d_1}\) chứa điểm \(\left( {0;1} \right).\) Miền nghiệm của bất phương trình \(3x + y \le 6\) là nửa mặt phẳng bờ \({d_2}:3x + y = 6\) chứa gốc tọa độ \(O\left( {0;0} \right).\) Miền nghiệm của bất phương trình \(x + y \le 4\) là nửa mặt phẳng bờ \({d_3}:x + y = 4\) chứa gốc tọa độ \(O\left( {0;0} \right).\) Miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{3x + y \le 6}\\{x + y \le 4}\end{array}} \right.\) là tứ giác \(OABC\) với \(A\left( {2;0} \right),\) \(B\left( {1;3} \right),\,\,C\left( {0;4} \right).\)
\(F\left( {1;3} \right) = 2.1 + 1,6.3 = 6,8;\) \(F\left( {0;4} \right) = 2.0 + 1,6.4 = 6,4.\) Vậy số tiền lãi lớn nhất phân xưởng này thu được trong một ngày là: 6,8 triệu đồng.
|