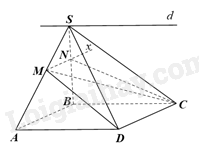
Giải bài 3 trang 117 sách bài tập toán 11 - Chân trời sáng tạo tập 1Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Tìm giao tuyến của các mặt phẳng: a) (SAD) và (SBC); b) (SAB) và (MDC), với M là một điểm bất kì thuộc cạnh SA. Đề bài Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Tìm giao tuyến của các mặt phẳng: a) (SAD) và (SBC); b) (SAB) và (MDC), với M là một điểm bất kì thuộc cạnh SA. Phương pháp giải - Xem chi tiết Sử dụng kiến thức về tính chất cơ bản về hai đường thẳng song song để tìm giao tuyến: Nếu hai mặt phẳng phân biệt lần lượt đi qua hai đường thẳng song song thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó. Lời giải chi tiết
a) Vì ABCD là hình bình hành nên AD//BC Ta có: \(S \in \left( {SAD} \right) \cap \left( {SBC} \right),AD \subset \left( {SAD} \right),BC \subset \left( {SBC} \right)\) và AD//BC nên giao tuyến của mặt phẳng (SAD) và (SBC) là đường thẳng d đi qua S song song với AD và BC. b) Vì ABCD là hình bình hành nên AB//DC Ta có: \(M \in \left( {SAB} \right) \cap \left( {MDC} \right),AB \subset \left( {SAB} \right),DC \subset \left( {MDC} \right)\) và AB//DC nên giao tuyến của mặt phẳng (SAB) và (MDC) là đường thẳng đi qua M song song với AB và DC.
|