Giải bài 5 trang 51 sách bài tập toán 11 - Chân trời sáng tạo tập 2Cho tứ diện đều ABCD cạnh a. Gọi O là tâm đường tròn ngoại tiếp tam giác BCD. Chứng minh rằng hai đường thẳng OA và CD vuông góc với nhau. Đề bài Cho tứ diện đều ABCD cạnh a. Gọi O là tâm đường tròn ngoại tiếp tam giác BCD. Chứng minh rằng hai đường thẳng OA và CD vuông góc với nhau. Phương pháp giải - Xem chi tiết Sử dụng kiến thức về hai đường thẳng vuông góc trong không gian. Lời giải chi tiết
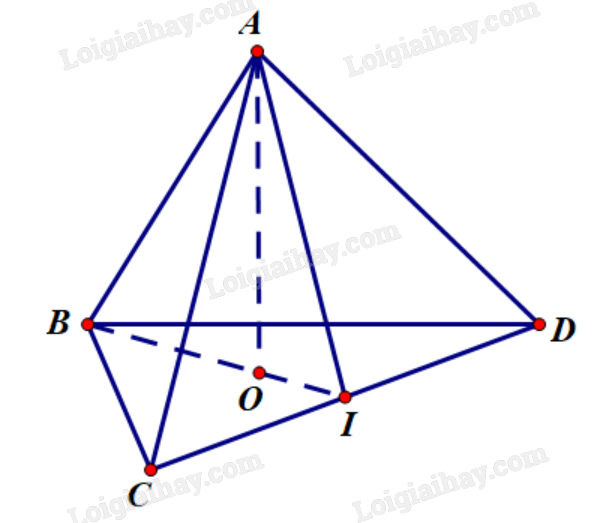
Gọi I là trung điểm của CD. Tứ diện đều có 4 mặt là tam giác đều. Vì O là tâm đường tròn ngoại tiếp tam giác BCD nên O là trọng tâm tam giác BCD. Ta có AI vừa là đường trung tuyến, vừa là đường cao của tam giác ACD; BI vừa là đường trung tuyến, vừa là đường cao của tam giác BCD (do đó O thuộc BI vì trọng tâm nằm trên đường trung tuyến). Khi đó, \(AI \bot CD\) và \(BI \bot CD\). Suy ra \(CD \bot (ABI)\), mà OA thuộc (ABI) nên \(CD \bot OA\).  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
