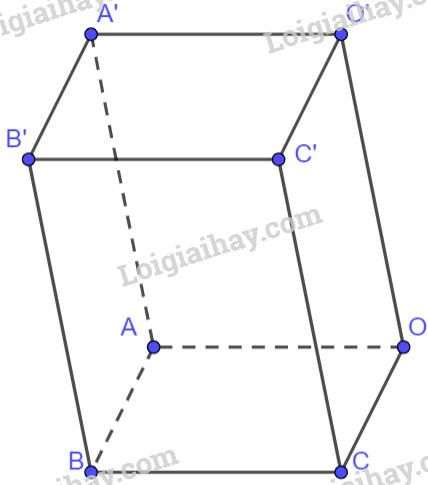
Giải bài tập 2.39 trang 74 SGK Toán 12 tập 1 - Kết nối tri thứcTrong không gian Oxyz, cho hình hộp OABC.O’A’B’C’ và các điểm (Aleft( {2;3;1} right),Cleft( { - 1;2;3} right)) và (O'left( {1; - 2;2} right)). Tìm tọa độ các đỉnh còn lại của hình hộp. Đề bài Trong không gian Oxyz, cho hình hộp OABC.O’A’B’C’ có \(A\left( {2;3;1} \right),C\left( { - 1;2;3} \right)\) và \(O'\left( {1; - 2;2} \right)\). Tìm tọa độ các đỉnh còn lại của hình hộp. Phương pháp giải - Xem chi tiết Trong không gian Oxyz, cho hình hộp OABC.O’A’B’C’ và các điểm \(A\left( {2;3;1} \right),C\left( { - 1;2;3} \right)\) và \(O'\left( {1; - 2;2} \right)\). Tìm tọa độ các đỉnh còn lại của hình hộp. Lời giải chi tiết
Ta có: O(0; 0; 0) Vì OABC.O’A’B’C’ là hình hộp nên \(\overrightarrow {AA'} = \overrightarrow {OO'} \Rightarrow \left\{ \begin{array}{l}{x_{A'}} - {x_A} = {x_{O'}} - {x_O}\\{y_{A'}} - {y_A} = {y_{O'}} - {y_O}\\{z_{A'}} - {z_A} = {z_{O'}} - {z_O}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_{A'}} = {x_{O'}} - {x_O} + {x_A} = 3\\{y_{A'}} = {y_{O'}} - {y_O} + {y_A} = 1\\{z_{A'}} = {z_{O'}} - {z_O} + {z_A} = 3\end{array} \right. \Rightarrow A'\left( {3;1;3} \right)\) \(\overrightarrow {CC'} = \overrightarrow {OO'} \Rightarrow \left\{ \begin{array}{l}{x_{C'}} - {x_C} = {x_{O'}} - {x_O}\\{y_{C'}} - {y_C} = {y_{O'}} - {y_O}\\{z_{C'}} - {z_C} = {z_{O'}} - {z_O}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_{C'}} = {x_{O'}} - {x_O} + {x_C} = 0\\{y_{C'}} = {y_{O'}} - {y_O} + {y_C} = 0\\{z_{C'}} = {z_{O'}} - {z_O} + {z_C} = 5\end{array} \right. \Rightarrow C'\left( {0;0;5} \right)\) Vì ABCO là hình bình hành nên \(\overrightarrow {CB} = \overrightarrow {OA} \Rightarrow \left\{ \begin{array}{l}{x_B} + 1 = 2\\{y_B} - 2 = 3\\{z_B} - 3 = 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_B} = 1\\{y_B} = 5\\{z_B} = 4\end{array} \right. \Rightarrow B\left( {1;5;4} \right)\) Vì OABC.O’A’B’C’ là hình hộp nên \(\overrightarrow {BB'} = \overrightarrow {OO'} \Rightarrow \left\{ \begin{array}{l}{x_{B'}} - 1 = 1\\{y_{B'}} - 5 = - 2\\{z_{B'}} - 4 = 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_{B'}} = 2\\{y_{B'}} = 3\\{z_{B'}} = 6\end{array} \right. \Rightarrow B'\left( {2;3;6} \right)\)
|