Giải mục 1 trang 71, 72 SGK Toán 11 tập 1 - Chân trời sáng tạoXét hàm số (y = fleft( x right) = frac{{2{x^2} - 2}}{{x - 1}}).
Lựa chọn câu để xem lời giải nhanh hơn
HĐ1 Trả lời câu hỏi Hoạt động 1 trang 71 SGK Toán 11 Chân trời sáng tạo Xét hàm số \(y = f\left( x \right) = \frac{{2{x^2} - 2}}{{x - 1}}\). a) Bảng sau đây cho biết giá trị của hàm số tại một số điểm gần điểm 1.
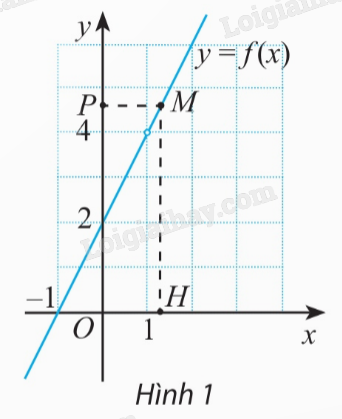
Có nhận xét gì về giá trị của hàm số khi \(x\) càng gần đến 1? b) Ở Hình 1, \(M\) là điểm trên đồ thị hàm số \(y = f\left( x \right)\); \(H\) và \(P\) lần lượt là hình chiếu của điểm \(M\) trên trục hoành và trục tung. Khi điểm \(H\) thay đổi gần về điểm \(\left( {1;0} \right)\) trên trục hoành thì điểm \(P\) thay đổi như thế nào?
Phương pháp giải: Quan sát đồ thị và nhận xét. Lời giải chi tiết: a) Khi \(x\) càng gần đến 1 thì giá trị của hàm số càng gần đến 4. b) Khi điểm \(H\) thay đổi gần về điểm \(\left( {1;0} \right)\) trên trục hoành thì điểm \(P\) càng gần đến điểm \(\left( {0;4} \right)\). TH1 Trả lời câu hỏi Thực hành 1 trang 72 SGK Toán 11 Chân trời sáng tạo Tìm các giới hạn sau: a) \(\mathop {\lim }\limits_{x \to 3} \left( {2{x^2} - x} \right)\); b) \(\mathop {\lim }\limits_{x \to - 1} \frac{{{x^2} + 2x + 1}}{{x + 1}}\). Phương pháp giải: Đưa về tính giới hạn của dãy số \(\left( {{x_n}} \right)\) thỏa mãn \({x_n} \to {x_0}\) khi \(n \to + \infty \). Lời giải chi tiết: a) Đặt \(f\left( x \right) = 2{x^2} - x\). Hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\). Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì thỏa mãn \({x_n} \to 3\) khi \(n \to + \infty \). Ta có: \(\lim f\left( {{x_n}} \right) = \lim \left( {2x_n^2 - {x_n}} \right) = 2.\lim x_n^2 - \lim {x_n} = {2.3^2} - 3 = 15\). Vậy \(\mathop {\lim }\limits_{x \to 3} \left( {2{x^2} - x} \right) = 15\). b) Đặt \(f\left( x \right) = \frac{{{x^2} + 2x + 1}}{{x + 1}}\). Hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\). Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì thỏa mãn \({x_n} \to - 1\) khi \(n \to + \infty \). Ta có: \(\lim f\left( {{x_n}} \right) = \lim \frac{{x_n^2 + 2{x_n} + 1}}{{{x_n} + 1}} = \lim \frac{{{{\left( {{x_n} + 1} \right)}^2}}}{{{x_n} + 1}} = \lim \left( {{x_n} + 1} \right) = \lim {x_n} + 1 = - 1 + 1 = 0\). Vậy \(\mathop {\lim }\limits_{x \to - 1} \frac{{{x^2} + 2x + 1}}{{x + 1}} = 0\).
|