Giải mục 2 trang 22, 23, 24 SGK Toán 12 tập 2 - Kết nối tri thứcỨng dụng tích phân để tính thể tích vật thể
Lựa chọn câu để xem lời giải nhanh hơn
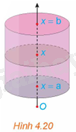
HĐ3 Trả lời câu hỏi Hoạt động 3 trang 22 SGK Toán 12 Kết nối tri thức Xét hình trụ có bán kính đáy R, có trục là trục hoành Ox, nằm giữa hai mặt phẳng \(x = a\) và \(x = b\left( {a < b} \right)\) (H.4.20).
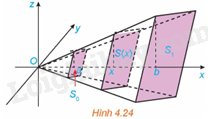
a) Tính thể tích V của hình trụ. b) Tính diện tích mặt cắt S(x) khi cắt hình trụ bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x \(\left( {a \le x \le b} \right)\). Từ đó tính \(\int\limits_a^b {S\left( x \right)dx} \) và so sánh với V. Phương pháp giải: Sử dụng kiến thức về thể tích hình trụ để tính: Hình trụ có bán kính đáy R và chiều cao h thì có thể tích là: \(V = \pi {R^2}h\). Lời giải chi tiết: a) Thể tích V của hình trụ là: \(V = \pi {R^2}h = \pi {R^2}\left( {b - a} \right)\) (h là chiều cao của hình trụ). b) Diện tích mặt cắt S(x) khi cắt hình trụ bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x là: \(S\left( x \right) = \pi {R^2}\). Ta có: \(\int\limits_a^b {S\left( x \right)dx} = \int\limits_a^b {\pi {R^2}dx} = \pi {R^2}x\left| \begin{array}{l}b\\a\end{array} \right. = \pi {R^2}\left( {b - a} \right)\). Do đó, \(V = \int\limits_a^b {S\left( x \right)dx} \). VD2 Trả lời câu hỏi Vận dụng 2 trang 23 SGK Toán 12 Kết nối tri thức Tính thể tích của khối chóp cụt đều có diện tích hai đáy là \({S_o},{S_1}\) và chiều cao bằng h (H.4.24). Từ đó suy ra công thức tính thể tích khối chóp đều có diện tích đáy bằng S và chiều cao bằng h.
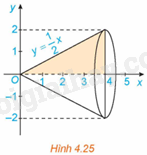
Phương pháp giải: Sử dụng kiến thức về công thức tính thể tích vật để để tính: Cho một vật thể trong không gian Oxyz. Gọi \(\beta \) là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm có hoành độ \(x = a,x = b\). Một mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x cắt vật thể theo mặt cắt có diện tích là S(x). Giả sử S(x) là hàm số liên tục trên đoạn [a; b]. Khi đó thể tích V của phần vật thể \(\beta \) được tính bởi công thức \(V = \int\limits_a^b {S\left( x \right)dx} \). Lời giải chi tiết: Trong hệ trục tọa độ Oxyz, ta đặt khối chóp (tạo ra khối chóp cụt) sao cho đường cao nằm trên trục Ox và đỉnh trùng với gốc tọa độ. Gọi a và b lần lượt là khoảng cách từ O đến đáy nhỏ và đáy lớn. Khi đó, chiều cao của khối chóp cụt là: \(h = b - a\). Thiết diện của khối chóp cụt đều cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x \(\left( {a \le x \le b} \right)\) là một đa giác đều đồng dạng với đáy lớn với tỉ số đồng dạng là \(\frac{x}{b}\). Ta có: \(\frac{{S\left( x \right)}}{{{S_1}}} = \frac{{{x^2}}}{{{b^2}}}\) nên \(S\left( x \right) = {S_1}.\frac{{{x^2}}}{{{b^2}}}\). Thể tích của khối chóp cụt đều là: \(V = \int\limits_a^b {{S_1}\frac{{{x^2}}}{{{b^2}}}dx} = \frac{{{S_1}\left( {{b^3} - {a^3}} \right)}}{{3{b^2}}} = \frac{{b - a}}{3}.\frac{{{S_1}{a^2} + {S_1}ab + {S_1}{b^2}}}{{{b^2}}} = \frac{h}{3}\left( {\frac{{{S_1}{a^2}}}{{{b^2}}} + \frac{{{S_1}a}}{b} + {S_1}} \right)\) Lại có: \({S_0} = S\left( a \right) = \frac{{{S_1}{a^2}}}{{{b^2}}},\frac{{{S_1}a}}{b} = \sqrt {{S_1}.\frac{{{S_1}{a^2}}}{{{b^2}}}} = \sqrt {{S_1}{S_0}} \). Do đó, \(V = \frac{h}{3}\left( {{S_0} + \sqrt {{S_0}{S_1}} + {S_1}} \right)\) Khối chóp đều được coi là khối chóp cụt đều có \({S_0} = 0\). Do đó, thể tích khối chóp đều có diện tích đáy bằng S và chiều cao bằng h là: \(V = \frac{1}{3}S.h\). HĐ4 Trả lời câu hỏi Hoạt động 4 trang 24 SGK Toán 12 Kết nối tri thức Xét hình phẳng giới hạn bởi đồ thị hàm số \(f\left( x \right) = \frac{1}{2}x\), trục hoành và hai đường thẳng \(x = 0,x = 4\). Khi quay hình phẳng này xung quanh trục hoành Ox ta được khối nón có đỉnh là gốc O, trục là Ox và đáy là hình tròn bán kính bằng 2 (H.4.25).
a) Tính thể tích V của khối nón. b) Khi cắt khối nón bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ bằng x \(\left( {0 \le x \le 4} \right)\) thì mặt cắt thu được là một hình tròn có bán kính là f(x), do đó diện tích mặt cắt là \(S\left( x \right) = \pi {f^2}\left( x \right)\). Tính \(\pi \int\limits_0^4 {{f^2}\left( x \right)dx} \) và so sánh với V. Phương pháp giải: Sử dụng kiến thức về thể tích khối nón để tính: Thể tích của khối nón có bán kính R, chiều cao h là: \(V = \frac{1}{3}\pi {R^2}h\). Lời giải chi tiết: a) Thể tích của khối nón là: \(V = \frac{1}{3}.\pi {.2^2}.4 = \frac{{16\pi }}{3}\). b)
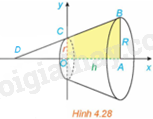
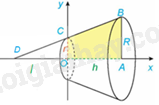
Khi cắt khối nón bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ bằng x \(\left( {0 \le x \le 4} \right)\) thì mặt cắt thu được là một hình tròn có bán kính là \(f\left( x \right) = \frac{1}{2}x\). Diện tích mặt cắt là: \(S\left( x \right) = \pi {f^2}\left( x \right) = \frac{1}{4}\pi {x^2}\). Ta có: \(\pi \int\limits_0^4 {{f^2}\left( x \right)dx} = \pi \int\limits_0^4 {\frac{1}{4}{x^2}dx = \frac{{\pi {x^3}}}{{12}}\left| \begin{array}{l}4\\0\end{array} \right. = } \frac{{16\pi }}{3}\). Do đó, \(V = \pi \int\limits_0^4 {{f^2}\left( x \right)dx} \). VD3 Trả lời câu hỏi Vận dụng 3 trang 25 SGK Toán 12 Kết nối tri thức a) Tính thể tích của khối tròn xoay sinh ra khi quay hình thang vuông OABC trong mặt phẳng Oxy với \(OA = h,AB = R\) và \(OC = r\), quanh trục Ox (H.4.28).
b) Từ công thức thu được ở phần a, hãy rút ra công thức tính thể tích của khối nón có bán kính đáy bằng R và chiều cao h. Phương pháp giải: Sử dụng kiến thức về công thức tính thể tích của khối tròn xoay để tính: Cho hàm số f(x) liên tục, không âm trên đoạn [a; b]. Khi quay hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b\) xung quanh trục hoành, ta được hình khối gọi là một khối tròn xoay. Khi cắt khối tròn xoay đó bởi một mặt phẳng vuông góc với trục Ox tại điểm \(x \in \left[ {a;b} \right]\) được một hình tròn có bán kính f(x). Thể tích của khối tròn xoay này là: \(V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \). Lời giải chi tiết: a)
Ta có: \(C\left( {0;r} \right),B\left( {h,R} \right) \Rightarrow \overrightarrow {BC} \left( { - h,r - R} \right) \Rightarrow \overrightarrow n \left( {r - R,h} \right)\) Phương trình đường thẳng BC là: \(\left( {r - R} \right)x + h\left( {y - r} \right) = 0 \Leftrightarrow y = \frac{{hr + \left( {R - r} \right)x}}{h}\) Thể tích hình cần tính là: \(V = \pi \int\limits_0^h {{{\left[ {\frac{{hr + \left( {R - r} \right)x}}{h}} \right]}^2}dx} = \pi \int\limits_0^h {{{\left[ {r + \frac{{\left( {R - r} \right)x}}{h}} \right]}^2}dx} = \pi \int\limits_0^h {\left[ {{r^2} + \frac{{2r\left( {R - r} \right)x}}{h} + \frac{{{{\left( {R - r} \right)}^2}{x^2}}}{{{h^2}}}} \right]dx} \) \( = \pi \left( {{r^2}x + \frac{{r\left( {R - r} \right){x^2}}}{h} + \frac{{{{\left( {R - r} \right)}^2}{x^3}}}{{3{h^2}}}} \right)\left| \begin{array}{l}h\\0\end{array} \right. = \pi \left( {{r^2}h + \frac{{r\left( {R - r} \right){h^2}}}{h} + \frac{{{{\left( {R - r} \right)}^2}{h^3}}}{{3{h^2}}}} \right)\) \( = \pi \left( {{r^2}h + r\left( {R - r} \right)h + \frac{{{{\left( {R - r} \right)}^2}h}}{3}} \right) = \pi \left( {{r^2}h + rRh - {r^2}h + \frac{{{R^2}h}}{3} - \frac{{2rRh}}{3} + \frac{{{r^2}h}}{3}} \right)\) \( = \pi \left( {\frac{{rRh}}{3} + \frac{{{R^2}h}}{3} + \frac{{{r^2}h}}{3}} \right) = \frac{1}{3}\pi h\left( {{R^2} + rR + {r^2}} \right)\). b) Khi \(r = 0\) thì khối nón cụt trở thành khối nón có chiều cao h và bán kính đáy R. Do đó, thể tích khối nón là: \(V = \frac{1}{3}\pi {R^2}h\).
|