Giải mục 2 trang 68, 69, 70, 71 SGK Toán 12 tập 1 - Cánh diềuTọa độ của một vecto GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho HocTot.XYZ và nhận về những phần quà hấp dẫn
Lựa chọn câu để xem lời giải nhanh hơn
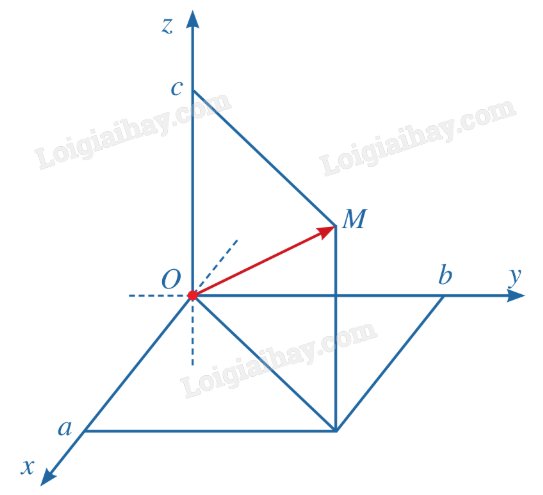
HĐ3 Trả lời câu hỏi Hoạt động 3 trang 68 SGK Toán 12 Cánh diều Cho điểm M trong không gian với hệ tọa độ Oxyz. a) Vẽ vecto \(\overrightarrow {OM} \). b) Nêu cách xác định tọa độ của điểm M. Lời giải chi tiết: a)
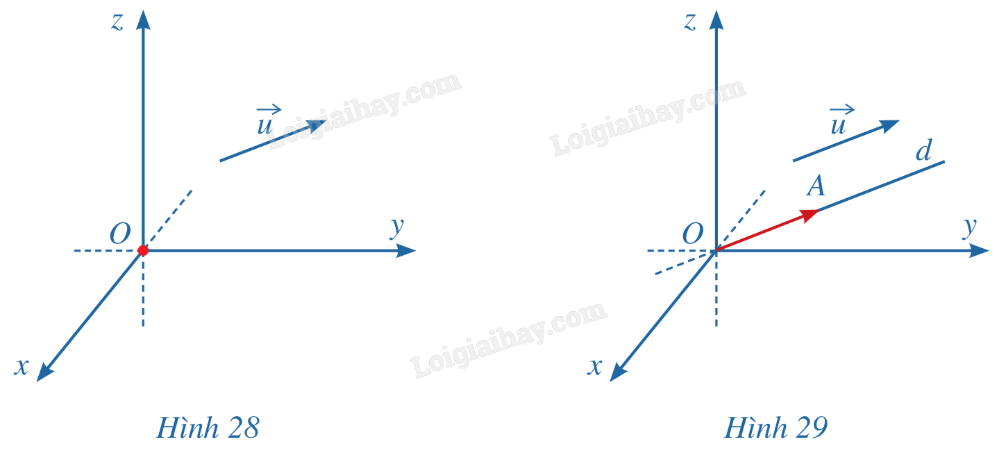
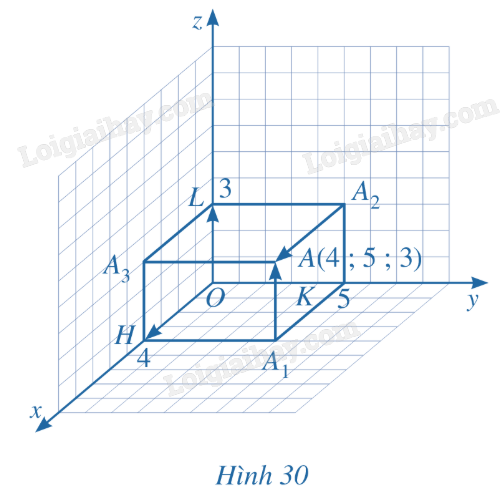
b) Nếu \(\overrightarrow {OM} \) có tọa độ (a;b;c) thì ta viết \(\overrightarrow {OM} = (a;b;c)\), trong đó a là hoành độ, b là tung độ và c là cao độ. LT3 Trả lời câu hỏi Luyện tập 3 trang 68 SGK Toán 12 Cánh diều Trong không gian với hệ tọa độ Oxyz, cho \(\overrightarrow {OA} = (3;1; - 2)\). Tìm tọa độ của điểm A. Phương pháp giải: Sử dụng định nghĩa: “Tọa độ của điểm M là tọa độ của vecto \(\overrightarrow {OM} \)”. Lời giải chi tiết: Vì \(\overrightarrow {OA} = (3;1; - 2)\) nên A(3;1;-2). HĐ4 Trả lời câu hỏi Hoạt động 4 trang 69 SGK Toán 12 Cánh diều Trong không gian với hệ tọa độ Oxyz, cho vecto \(\vec u\) (Hình 28). Hãy xác định điểm A sao cho \(\overrightarrow {OA} = \vec u\). Phương pháp giải: Vẽ \(\overrightarrow {OA} \) có tung độ, hoành độ và cao độ giống nhau. Lời giải chi tiết: Cách xác định điểm A: - Từ gốc tọa độ O, dựng đường thẳng d song song với giá của vecto \(\overrightarrow u \). - Trên d, lấy điểm A sao cho vecto \(\overrightarrow {OA} \) cùng hướng với vecto \(\overrightarrow u \) và \(OA = \left| {\overrightarrow u } \right|\). Vậy ta được điểm A thỏa mãn \(\overrightarrow {OA} = \overrightarrow u \). LT4 Trả lời câu hỏi Luyện tập 4 trang 69 SGK Toán 12 Cánh diều Tìm tọa độ của các vecto \(\overrightarrow {KA} \), \(\overrightarrow {{A_3}A} \) ở Hình 30.
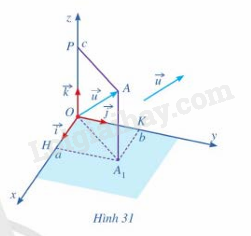
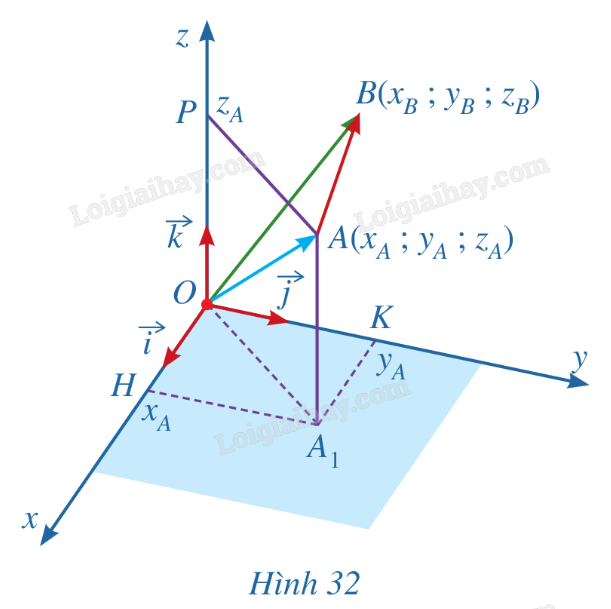
Phương pháp giải: Sử dụng định nghĩa: - Tọa độ của điểm M là tọa độ của vecto \(\overrightarrow {OM} \). - Tọa độ của \(\overrightarrow u \) là tọa độ của điểm A, trong đó A là điểm sao cho \(\overrightarrow {OA} = \overrightarrow u \). Lời giải chi tiết: Quan sát Hình 30, có \(\overrightarrow {KA} = \overrightarrow {O{A_3}} \), \(\overrightarrow {{A_3}A} = \overrightarrow {OK} \). Mặt khác, vì \({A_3}(4;0;3)\) và \(K(0;5;0)\) nên \(\overrightarrow {O{A_3}} = (4;0;3)\), \(\overrightarrow {OK} = (0;5;0)\). Do đó \(\overrightarrow {KA} = (4;0;3)\), \(\overrightarrow {{A_3}A} = (0;5;0)\). HĐ5 Trả lời câu hỏi Hoạt động 5 trang 70 SGK Toán 12 Cánh diều Trong không gian với hệ tọa độ Oxyz, cho vecto \(\vec u = \left( {a;b;c} \right)\) (Hình 31). Lấy điểm A sao cho \(\overrightarrow {OA} = \vec u\). a) Tìm hoành độ, tung độ và cao độ của điểm A. b) Biểu diễn vecto \(\overrightarrow {OH} \) qua vecto \(\vec i\), vecto \(\overrightarrow {OK} \) qua vecto \(\vec j\), vecto \(\overrightarrow {OP} \) qua vecto \(\vec k\). c) Biểu diễn vecto \(\vec u\) theo các vecto \(\vec i,\vec j,\vec k\).
Phương pháp giải: Áp dụng quy tắc tính tọa độ vecto. Lời giải chi tiết: a) a là hoành độ của điểm A, b là tung độ của điểm A, c là cao độ của điểm A. b) \(\overrightarrow {OH} = a\overrightarrow {i} \), \(\overrightarrow {OK} = b\overrightarrow {j} \), \(\overrightarrow {OP} = c\overrightarrow {k} \). c) Áp dụng quy tắc hình hộp ta được: \(\vec u = a\overrightarrow {i} + b\overrightarrow {j} + c\overrightarrow {k}\). LT5 Trả lời câu hỏi Luyện tập 5 trang 70 SGK Toán 12 Cánh diều Trong không gian với hệ tọa độ Oxyz, cho vecto \(\overrightarrow {OB} = - \overrightarrow i + 2\overrightarrow k \) và vecto \(\overrightarrow v = - 7\overrightarrow j + \overrightarrow k \). Hãy tìm tọa độ của: a) Điểm B; b) Vecto \(\overrightarrow v \). Phương pháp giải: Sử dụng định nghĩa: - Trong không gian với hệ tọa độ Oxyz, nếu \(\overrightarrow u = (a;b;c)\) thì \(\overrightarrow u = a\overrightarrow i + b\overrightarrow j + c\overrightarrow k \). - Tọa độ của điểm M là tọa độ của vecto \(\overrightarrow {OM} \). Lời giải chi tiết: a) \(\overrightarrow {OB} = - \overrightarrow i + 2\overrightarrow k = ( - 1;0;2)\). Do đó B(-1;0;2). b) \(\overrightarrow v = - 7\overrightarrow j + \overrightarrow k = (0; - 7;1)\). HĐ6 Trả lời câu hỏi Hoạt động 6 trang 71 SGK Toán 12 Cánh diều Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(A({x_A};{y_A};{z_A})\), \(B({x_B};{y_B};{z_B})\). a) Biểu diễn mỗi vecto \(\overrightarrow {OA}\), \(\overrightarrow {OB} \) theo các vecto \(\overrightarrow i\), \(\overrightarrow j \) và \(\overrightarrow k \). b) Tìm liên hệ giữa \(\overrightarrow {AB} \) và \(({x_B} - {x_A}).\vec i + ({y_B} - {y_A}).\vec j + ({z_B} - {z_A}).\vec k\). c) Từ đó, tìm tọa độ vecto \(\overrightarrow {AB} \).
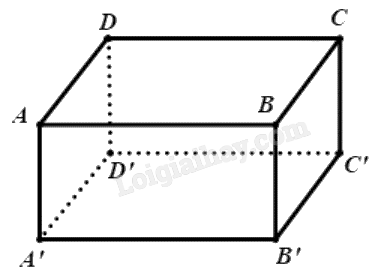
Phương pháp giải: Sử dụng lý thuyết tọa độ của vecto trong không gian. Lời giải chi tiết: a) \(\overrightarrow {OA} = \overrightarrow {O{A_1}} + \overrightarrow {OP} = \overrightarrow {OH} + \overrightarrow {OK} = {x_A}.\overrightarrow i + {y_A}.\overrightarrow j + {z_A}.\overrightarrow k \). Tương tự, ta có: \(\overrightarrow {OB} = {x_B}.\overrightarrow i + {y_B}.\overrightarrow j + {z_B}.\overrightarrow k \). b) Ta có: \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = {x_B}.\overrightarrow i + {y_B}.\overrightarrow j + {z_B}.\overrightarrow k - ({x_A}.\overrightarrow i + {y_A}.\overrightarrow j + {z_A}.\overrightarrow k ) = ({x_B} - {x_A}).\overrightarrow i + ({y_B} - {y_A}).\overrightarrow j + ({z_B} - {z_A}).\overrightarrow k \). c) Tọa độ vecto \(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A})\). LT6 Trả lời câu hỏi Luyện tập 6 trang 71 SGK Toán 12 Cánh diều Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD.A’B’C’D’ có A’(1;0;1), B’(2;1;2), D’(1;-1;1), C(4;5;-5). Tìm tọa độ đỉnh A của hình hộp. Phương pháp giải: Áp dụng quy tắc hình hộp và định lí về tọa độ của vecto: \(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A})\). Lời giải chi tiết:
Gọi A(x;y;z). Vì ABCD.A’B’C’D’ là hình hộp nên \(\overrightarrow {A'B'} + \overrightarrow {A'D'} + \overrightarrow {A'A} = \overrightarrow {A'C} \). Ta có \(\overrightarrow {A'B'} = (1;1;1)\), \(\overrightarrow {A'D'} = (0; - 1;0)\), \(\overrightarrow {A'A} = (x - 1;y;z - 1)\), \(\overrightarrow {A'C} = (3;5; - 6)\). Suy ra \(\left\{ \begin{array}{l}1 + 0 + (x - 1) = 3\\1 - 1 + y = 5\\1 + 0 + (z - 1) = - 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 5\\z = - 6\end{array} \right. \Rightarrow A(3;5; - 6)\).
|