Giải mục 3 trang 10, 11 SGK Toán 11 tập 1 - Chân trời sáng tạoTrong mặt phẳng tọa độ Oxy, vẽ đường tròn tâm O bán kính bằng 1 và điểm A(1; 0). a) Cho điểm B(0; 1). Số đo góc lượng giác (OA; OB) bằng bao nhiêu radian?
Lựa chọn câu để xem lời giải nhanh hơn
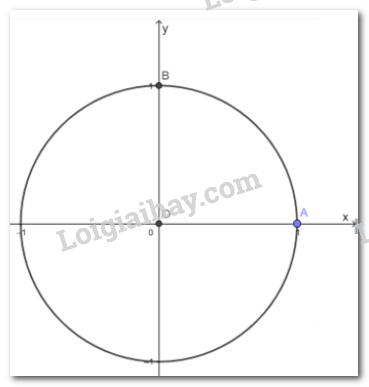
HĐ4 Trả lời câu hỏi Hoạt động 4 trang 11 SGK Toán 11 Chân trời sáng tạo Trong mặt phẳng tọa độ Oxy, vẽ đường tròn tâm O bán kính bằng 1 và điểm A(1; 0). a) Cho điểm B(0; 1). Số đo góc lượng giác (OA, OB) bằng bao nhiêu radian? b) Xác định các điểm A’ và B’ trên đường tròn sao cho các góc lượng giác (OA, OA’), (OA, OB’) có số đo lần lượt là \(\pi \) và \( - \frac{\pi }{2}\). Phương pháp giải: Vẽ đường tròn rồi nhận biết từng góc. Lời giải chi tiết: a) Góc lượng giác \(\left( {OA;OB} \right) = 90^\circ = \frac{\pi }{2}\). b) TH3 Trả lời câu hỏi Thực hành 3 trang 11 SGK Toán 11 Chân trời sáng tạo Biểu diễn trên đường tròn lượng giác các góc lượng giác có số đo là: a) \( - {1485^ \circ }\). b) \(\frac{{19\pi }}{4}\). Phương pháp giải: Xác định góc lượng giác trên vòng tròn lượng giác. Lời giải chi tiết: a) Ta có \( - {1485^ \circ } = - {45^ \circ } + ( - 4){.360^ \circ }\). Vậy điểm biểu diễn góc lượng giác có số đo \( - {1485^ \circ }\) là điểm M trên đường tròn lượng giác thuộc góc phần tư thứ IV sao cho \(\widehat {AMO} = {45^ \circ }\). b) Ta có \(\frac{{19\pi }}{4} = \frac{{3\pi }}{4} + 4\pi \). Vậy điểm biểu diễn góc lượng giác có số đo \(\frac{{19\pi }}{4}\) là điểm N trên phần đường tròn lượng giác thuộc góc phần tư thứ II sao cho \(\widehat {AMO} = \frac{{3\pi }}{4}\).
|