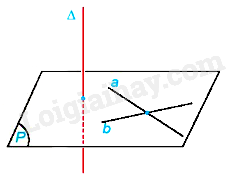
Lý thuyết Đường thẳng vuông góc với mặt phẳng - Toán 11 Kết nối tri thức1. Đường thẳng vuông góc với mặt phẳng 1. Đường thẳng vuông góc với mặt phẳng Đường thẳng \(\Delta \) được gọi là vuông góc với mặt phẳng (P) nếu \(\Delta \) vuông góc với mọi đường thẳng nằm trong (P). Chú ý: Khi \(\Delta \) vuông góc với (P), ta còn nói (P) vuông góc với \(\Delta \) hoặc \(\Delta \) và (P) vuông góc với nhau, kí hiệu \(\Delta \bot \left( P \right)\). 2. Điều kiện để đường thẳng vuông góc với mặt phẳng Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó.
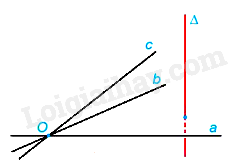
3. Tính chất - Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước. Nhận xét: Nếu ba đường thẳng đôi một phân biệt a, b, c cùng đi qua một điểm O và cùng vuông góc với một đường thẳng \(\Delta \) thì ba đường thẳng đó cùng nằm trong mặt phẳng đi qua O và vuông góc với \(\Delta \).
Chú ý: Mặt phẳng đi qua trung điểm của đoạn thẳng AB và vuông góc với đường thẳng AB được gọi là mặt phẳng trung trực của đoạn thẳng AB. Mặt phẳng trung trực của đoạn thẳng AB là tập hợp các điểm cách đều hai điểm A, B. - Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước. 4. Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng - Nếu đường thẳng a vuông góc với mặt phẳng (P) và mặt phẳng (P) thì các đường thẳng song song với a cũng vuông góc với (P). - Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau. - Nếu đường thẳng \(\Delta \) vuông góc với mặt phẳng (P) thì \(\Delta \) cũng vuông góc với các mặt phẳng song song với (P). - Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau. - Nếu đường thẳng \(\Delta \) vuông góc với mặt phẳng (P) thì \(\Delta \) vuông góc với mọi đường thẳng song song với (P). - Nếu đường thẳng a và mặt phẳng (P) cùng vuông góc với một đường thẳng \(\Delta \) thì a nằm trong (P) hoặc song song với (P).
|