Lý thuyết Hàm số mũ. Hàm số lôgarit - Toán 11 Chân trời sáng tạo1. Hàm số mũ - Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) được gọi là hàm số mũ cơ số a. 1. Hàm số mũ - Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) được gọi là hàm số mũ cơ số a. - Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) có: + Tập xác định: \(D = \mathbb{R}\). + Tập giá trị: \(T = \left( {0; + \infty } \right)\). + Hàm số liên tục trên \(\mathbb{R}\). + Sự biến thiên:
+ Đồ thị:
2. Hàm số lôgarit - Hàm số \(y = {\log _a}x\left( {a > 0;a \ne 1} \right)\) được gọi là hàm số lôgarit cơ số a. - Hàm số \(y = {\log _a}x\left( {a > 0;a \ne 1} \right)\) có: + Tập xác định: \(D = \left( {0; + \infty } \right)\). + Tập giá trị: \(T = \mathbb{R}\). + Hàm số liên tục trên \(\left( {0; + \infty } \right)\). + Sự biến thiên:
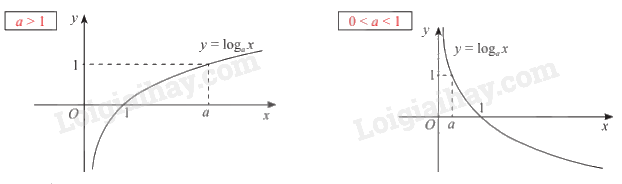
+ Đồ thị:
|