1. Nhận biết tính đơn điệu của hàm số bằng dấu của đạo hàm
Định lý 1
|
Cho hàm số y = f(x) có đạo hàm trên tập \(K \subset R\), trong đó K là một khoảng, đoạn hoặc nửa khoảng.
- Nếu f’(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K.
- Nếu f’(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên K.
|
Ví dụ: Hàm số y = |x| đồng biến trên khoảng \(\left( {0; + \infty } \right)\), nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\)
Định lý 2
|
Cho hàm số y = f(x) có đạo hàm trên tập \(K \subset R\), trong đó K là một khoảng, đoạn hoặc nửa khoảng. Nếu f’(x) \( \ge \) 0 (hoặc f’(x) \( \le \) 0) với mọi x thuộc K và f’(x) = 0 chỉ tại một số hữa hạn điểm của K thì hàm số f(x) đồng biến (hoặc nghịch biến) trên K.
|
Ví dụ: Hàm số \(y = {x^2} - 4x + 2\) có y’ = 2x – 4.
y’ > 0 với \(x \in (2; + \infty )\) nên HS đồng biến trên khoảng \(\left( {2; + \infty } \right)\).
y’ < 0 với \(x \in ( - \infty ;2)\) nên HS đồng biến trên khoảng \(\left( { - \infty ;2} \right)\).
2. Điểm cực trị, giá trị cực trị của hàm số
Khái niệm cực trị của hàm số
|
Cho hàm số y = f(x) liên tục trên tập \(K \subset R\), trong đó K là một khoảng, đoạn hoặc nửa khoảng và \({x_0} \in K,{x_1} \in K\).
- \({x_0}\) được gọi là một điểm cực đại của hàm số đã cho nếu tồn tại một khoảng (a;b) chứa điểm \({x_0}\) sao cho (a;b) \( \subset \) K và \(f(x) < f({x_0})\) với mọi \(x \in (a;b)\) và \(x \ne {x_0}\). Khi đó, \(f({x_0})\) được gọi là giá trị cực đại của hàm số đã cho, kí hiệu là \({f_{CĐ}}\).
- \({x_1}\) được gọi là một điểm cực tiểu của hàm số đã cho nếu tồn tại một khoảng (a;b) chứa điểm \({x_1}\) sao cho (c;d) \( \subset \) K và \(f(x) > f({x_1})\) với mọi \(x \in (c;d)\) và \(x \ne {x_1}\). Khi đó, \(f({x_1})\) được gọi là giá trị cực đại của hàm số đã cho, kí hiệu là \({f_{CT}}\).
Điểm cực đại và điểm cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại và giá trị cực tiểu được gọi chung là giá trị cực trị (hay cực trị).
|
Ví dụ: Cho đồ thị của hàm số y = f(x) như sau:
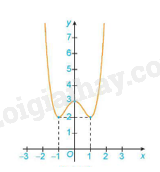
Hàm số đạt cực tiểu tại \(x = -1\) và \({y_{CT}}= y(-1) = 2\).
Hàm số đạt cực đại tại \(x = 0\) và \( y(0) = 3\).
Hàm số đạt cực tiểu tại \(x = 1\) và \({y_{CT}}= y(1) = 2\).
Định lý
|
Giả sử hàm số y = f(x) liên tục trên khoảng (a;b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Khi đó:
a) Nếu f’(x) < 0 với mọi \(x \in \left( {a;{x_0}} \right)\) và f’(x) > 0 với mọi \(x \in \left( {{x_0};b} \right)\) thì hàm số f(x) đạt cực tiểu tại điểm \({x_0}\).
b) Nếu f’(x) > 0 với mọi \(x \in \left( {a;{x_0}} \right)\) và f’(x) < 0 với mọi \(x \in \left( {{x_0};b} \right)\) thì hàm số f(x) đạt cực tiểu tại điểm \({x_0}\).
|
Ví dụ: Tìm cực trị của hàm số \(y = {x^3} - 6{x^2} + 9x + 30\).
Tập xác định của hàm số là R.
Ta có: \(y' = 3{x^2} - 12x + 9\); \(y’ = 0 \Leftrightarrow x = 1\) hoặc \(x = 3\).
Bảng biến thiên:
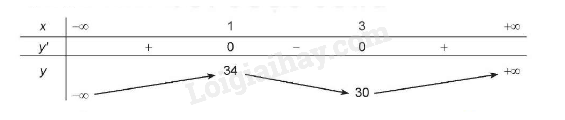
Hàm số đạt cực đại tại \(x = 1\) và \(y(1) = 34\).
Hàm số đạt cực tiểu tại \(x = 3\) và \({y_{CT}}= y(3) = 30\).