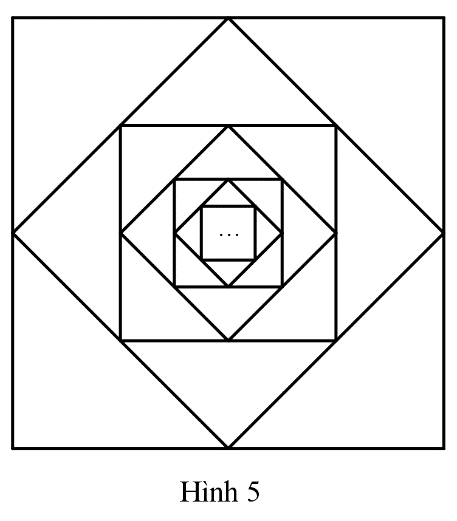
Bài 4 trang 70 SGK Toán 11 tập 1 - Chân trời sáng tạo

Đề bài

Từ hình vuông đầu tiên có cạnh bằng 1 (đơn vị độ dài), nối các trung điểm của bốn cạnh để có hình vuông thứ hai. Tiếp tục nối các trung điểm của bốn cạnh của hình vuông thứ hai để được hình vuông thứ ba. Cứ tiếp tục làm như thế, nhận được một dãy hình vuông (xem Hình 5).

a) Kí hiệu ${a_n}$ là diện tích của hình vuông thứ $n$ và ${S_n}$ là tổng diện tích của $n$ hình vuông đầu tiên. Viết công thức tính ${a_n},{S_n}\left( {n = 1,2,3,...} \right)$ và tìm $\lim {S_n}$ (giới hạn này nếu có được gọi là tổng diện tích của các hình vuông).

b) Kí hiệu ${p_n}$ là chu vi của hình vuông thứ $n$ và ${Q_n}$ là tổng chu vi của $n$ hình vuông đầu tiên. Viết công thức tính ${p_n}$ và ${Q_n}\left( {n = 1,2,3,...} \right)$ và tìm $\lim {Q_n}$ (giới hạn này nếu có được gọi là tổng chu vi của các hình vuông).

Lời giải chi tiết

a) Gọi ${u_n}$ là độ dài cạnh của hình vuông thứ n.

Đường chéo của hình vuông thứ n có độ dài là ${u_n}\sqrt 2$.

Độ dài cạnh hình vuông thứ n + 1 bằng nửa độ dài đường chéo hình vuông thứ n nên ta có:

${u_{n + 1}} = \frac{{{u_n}\sqrt 2 }}{2} = {u_n}.\frac{1}{{\sqrt 2 }}$.

Từ đó ta thấy $\left( {{u_n}} \right)$ là một cấp số nhân có số hạng đầu ${u_1} = 1$, công bội $q = \frac{1}{{\sqrt 2 }}$.

Vậy ${u_n} = {u_1}.{q^{n - 1}} = 1.{\left( {\frac{1}{{\sqrt 2 }}} \right)^{n - 1}} = \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}},n = 1,2,3,...$

Diện tích của hình vuông thứ $n$ là: ${a_n} = u_n^2 = {\left( {\frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}}} \right)^2} = \frac{1}{{{2^{n - 1}}}},n = 1,2,3,...$

Vậy ${S_n} = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}}$

Đây là tổng của cấp số nhân có số hạng đầu ${u_1} = 1$, công bội $q = \frac{1}{2}$.

Vậy ${S_n} = 1.\frac{{1 - {{\left( {\frac{1}{2}} \right)}^n}}}{{1 - \frac{1}{2}}} = 2\left( {1 - \frac{1}{{{2^n}}}} \right)$.

$\lim {S_n} = \lim 2\left( {1 - \frac{1}{{{2^n}}}} \right) = 2\left( {1 - \lim \frac{1}{{{2^n}}}} \right) = 2\left( {1 - 0} \right) = 2$.

b) Chu vi của hình vuông thứ $n$ là: ${p_n} = 4{u_n} = 4.\frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}} = \frac{4}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}},n = 1,2,3,...$

Vậy ${Q_n} = 4 + \frac{4}{{\sqrt 2 }} + \frac{4}{{{{\left( {\sqrt 2 } \right)}^2}}} + ... + \frac{4}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}} = 4\left( {1 + \frac{1}{{\sqrt 2 }} + \frac{1}{{{{\left( {\sqrt 2 } \right)}^2}}} + ... + \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}}} \right)$

$1 + \frac{1}{{\sqrt 2 }} + \frac{1}{{{{\left( {\sqrt 2 } \right)}^2}}} + ... + \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}}$ là tổng của cấp số nhân có số hạng đầu ${u_1} = 1$, công bội $q = \frac{1}{{\sqrt 2 }}$.

Vậy $1 + \frac{1}{{\sqrt 2 }} + \frac{1}{{{{\left( {\sqrt 2 } \right)}^2}}} + ... + \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}} = 1.\frac{{1 - {{\left( {\frac{1}{{\sqrt 2 }}} \right)}^n}}}{{1 - \frac{1}{{\sqrt 2 }}}} = \left( {2 + \sqrt 2 } \right)\left( {1 - \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right)$.

$\Rightarrow {Q_n} = 4\left( {2 + \sqrt 2 } \right)\left( {1 - \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right)$

$\begin{array}{l}\lim {Q_n} = \lim 4\left( {2 + \sqrt 2 } \right)\left( {1 - \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right) = 4\left( {2 + \sqrt 2 } \right)\left( {1 - \lim \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right)\\ = 4\left( {2 + \sqrt 2 } \right)\left( {1 - 0} \right) = 4\left( {2 + \sqrt 2 } \right)\end{array}$.