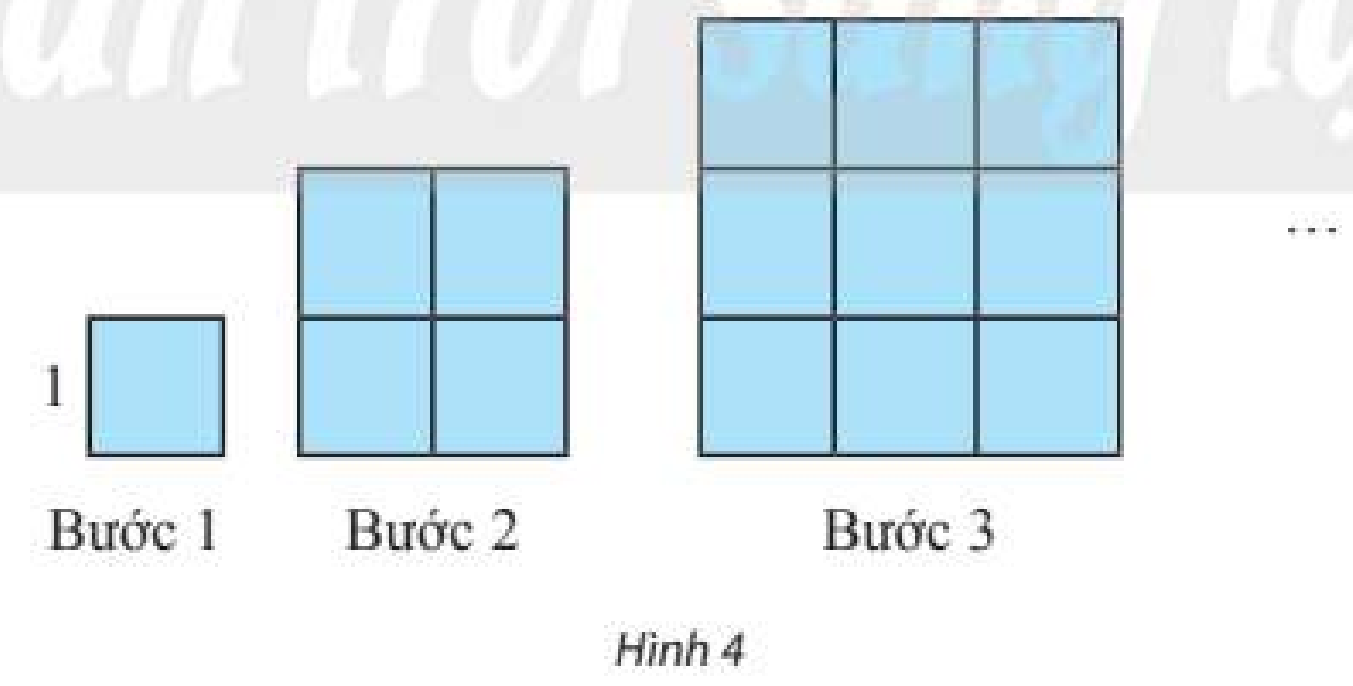
Giải mục 4 trang 68 SGK Toán 11 tập 1 - Chân trời sáng tạoDựng một dãy hình vuông bằng cách ghép từ các hình vuông đơn vị (cạnh bằng 1 đơn vị độ dài) theo các bước như Hình 4. Kí hiệu ({u_n}) (đơn vị diện tích) là diện tích hình vuông dựng được ở bước thứ (n).
Lựa chọn câu để xem lời giải nhanh hơn
HĐ5 Trả lời câu hỏi Hoạt động 5 trang 68 SGK Toán 11 Chân trời sáng tạo Dựng một dãy hình vuông bằng cách ghép từ các hình vuông đơn vị (cạnh bằng 1 đơn vị độ dài) theo các bước như Hình 4. Kí hiệu \({u_n}\) (đơn vị diện tích) là diện tích hình vuông dựng được ở bước thứ \(n\).
a) Với \(n\) như thế nào thì \({u_n}\) vượt quá 10000; 1000000? b) Cho hình có diện tích \(S\). Với \(n\) như thế nào thì \({u_n}\) vượt quá \(S\)? Phương pháp giải: a) Tìm công thức tổng quát của \({u_n}\) sau đó giải bất phương trình \({u_n} > 10000,{u_n} > 1000000\). b) Giải bất phương trình \({u_n} > S\). Lời giải chi tiết: a) Ta có: \({u_1} = {1^2};{u_2} = {2^2};{u_3} = {3^2};...;{u_n} = {n^2}\). \({u_n} > 10000 \Leftrightarrow {n^2} > 10000 = {100^2} \Leftrightarrow n > 100\). \({u_n} > 1000000 \Leftrightarrow {n^2} > 1000000 = {1000^2} \Leftrightarrow n > 1000\). b) \({u_n} > S \Leftrightarrow {n^2} > S \Leftrightarrow n > \sqrt S \). Vậy với các số tự nhiên \(n > \sqrt S \) thì \({u_n} > S\).
|