Nội dung từ Loigiaihay.Com
Cho hình lập phươngABCD.A′B′C′D′. Gọi α là góc giữa AC′ và mp (A′BCD′). Chọn khẳng định đúng trong các khẳng định sau?
-
A.
α=300.
-
B.
tanα=2√3.
-
C.
α=450.
-
D.
tanα=√2.
- Tìm giao điểm I của AC′ với (A′BCD′).
- Tìm hình chiếu H của C′ trên (A′BCD′) bằng cách tìm một đường thẳng qua C′ mà vuông góc với (A′BCD′).
- Góc cần tìm là góc giữa C′I và hình chiếu HI của nó trên mặt phẳng (A′BCD′).
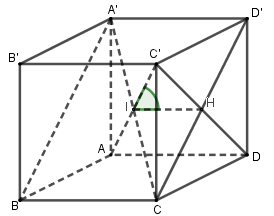
Gọi {A′C∩AC′=IC′D∩CD′=H
mà {C′D⊥CD′C′D⊥A′D′⇒C′D⊥(A′BCD′)⇒IH là hình chiếu vuông góc của IC′ lên (A′BCD′)⇒^C′IHlà góc giữa IC′ và (A′BCD′) và cũng là góc giữa AC′ và (A′BCD′). Mà tan^C′IH=C′HIH=1√2.2=√2.
Đáp án : D

Các bài tập cùng chuyên đề
Cho tứ diện ABCD có cạnh AB, BC, CD bằng nhau và vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng?
-
A.
Góc giữa AC và (BCD) là góc ACB.
-
B.
Góc giữa AD và (ABC) là góc ADB.
-
C.
Góc giữa AC và (ABD) là góc CAB.
-
D.
Góc giữa CD và (ABD) là góc CBD.
Cho tam giác ABC vuông cân tại A và BC=a. Trên đường thẳng qua A vuông góc với (ABC) lấy điểm S sao cho SA=a√62. Tính số đo góc giữa đường thẳng SA và (ABC)
-
A.
30∘.
-
B.
45∘.
-
C.
60∘.
-
D.
90∘.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC=a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểmBC. Biết SB=a. Tính số đo của góc giữa SA và (ABC).
-
A.
30∘.
-
B.
45∘.
-
C.
60∘.
-
D.
75∘.
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh bằng a và SA⊥(ABCD). Biết SA=a√63. Tính góc giữa SC và (ABCD).
-
A.
30∘.
-
B.
45∘.
-
C.
60∘.
-
D.
75∘.
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và (ABC).
-
A.
600
-
B.
750
-
C.
450
-
D.
300
Trong các mệnh đề sau mệnh đề nào đúng?
-
A.
Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng đã cho
-
B.
Nếu a và b song song (hoặc a trùng với b) thì góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường thẳng b và mặt phẳng (P) .
-
C.
Nếu góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường thẳng a và mặt phẳng (Q) thì mặt phẳng (P) song song với mặt phẳng (Q).
-
D.
Góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường thẳng b và mặt phẳng (P) thì a song song với b.
Cho hình chóp S.ABCD có SA⊥(ABCD) và đáy ABCD là hình chữ nhật. Gọi O là tâm của ABCD và I là trung điểm của SC. Khẳng định nào sau đây sai ?
-
A.
IO⊥(ABCD).
-
B.
BC⊥SB.
-
C.
(SAC) là mặt phẳng trung trực của đoạn BD.
-
D.
Tam giác SCD vuông ở D.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA⊥(ABCD), SA=a√6. Gọi α là góc giữa SC và mp(SAB). Chọn khẳng định đúng trong các khẳng định sau?
-
A.
tanα=1√8.
-
B.
tanα=1√7.
-
C.
α=300.
-
D.
tanα=1√6.
Cho hình chóp S.ABDC, với đáy ABCD là hình bình hành tâm O;AD,SA,AB đôi một vuông góc AD=8,SA=6. (P) là mặt phẳng qua trung điểm của AB và vuông góc với AB. Thiết diện của (P) và hình chóp có diện tích bằng?
-
A.
36
-
B.
16
-
C.
17
-
D.
18
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và SA=SB=SC=b. Gọi G là trọng tâm ΔABC. Độ dài SG là:
-
A.
√9b2+3a23.
-
B.
√b2−3a23.
-
C.
√9b2−3a23.
-
D.
√b2+3a23.
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và SA=SB=SC=b. Gọi G là trọng tâm ΔABC. Xét mặt phẳng (P) đi qua A và vuông góc với SC. Tìm hệ thức liên hệ giữa a và b để (P) cắt SC tại điểm C1 nằm giữa S và C.
-
A.
b>a√2.
-
B.
b<a√2.
-
C.
a<b√2.
-
D.
a>b√2.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều có đường cao SH vuông góc với mp(ABCD). Gọi α là góc giữa BD và mp(SAD). Chọn khẳng định đúng trong các khẳng định sau?
-
A.
α=600.
-
B.
α=300.
-
C.
cosα=√32√2.
-
D.
sinα=√32√2.
Cho tứ diện ABCD đều. Gọi α là góc giữa AB và mp(BCD). Chọn khẳng định đúng trong các khẳng định sau?
-
A.
cosα=√33.
-
B.
cosα=√34.
-
C.
cosα=0.
-
D.
cosα=√32.
Cho hình lập phương ABCD.A1B1C1D1. Gọi α là góc giữa AC1 và mp(ABCD). Chọn khẳng định đúng trong các khẳng định sau?
-
A.
α=450
-
B.
tanα=1√2
-
C.
tanα=2√3
-
D.
α=300
Cho hình thoi ABCD có tâm O,^ADC=600,AC=2a. Lấy điểm S không thuộc (ABCD) sao cho SO⊥(ABCD). Gọi α là góc giữa đường thẳng SB và mặt phẳng (ABCD) và tanα=12. Gọi β là góc giữa SC và (ABCD), chọn mệnh đề đúng :
-
A.
sinβ=12.
-
B.
cotβ=√32.
-
C.
tanβ=√32.
-
D.
β=600.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB=a, BC=2a, SA vuông góc với mặt phẳng đáy và SA=√15a (tham khảo hình bên)
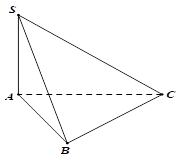
Góc giữa đường thẳng SC và mặt phẳng đáy bằng
-
A.
90∘.
-
B.
45∘.
-
C.
30∘.
-
D.
60∘.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với (ABCD) và SA=2a. Gọi G là trọng tâm tam giác SAB, α là góc tạo bởi đường thẳng CG và mặt phẳng (SAC). Tính sinα.
-
A.
√1717
-
B.
1√34
-
C.
2√17
-
D.
2√34












