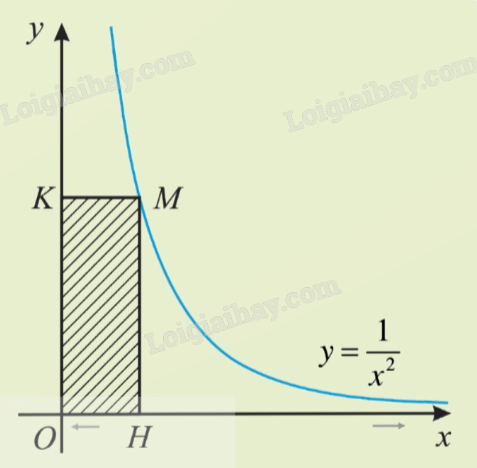
Giải câu hỏi mở đầu trang 71 SGK Toán 11 tập 1 - Chân trời sáng tạo

Đề bài

Quan sát hình bên, cho biết hình chữ nhật OHMK thay đổi nhưng điểm M luôn nằm trên đồ thị hàm số  \(y = \frac{1}{{{x^2}}}\) (x > 0). Diện tích hình chữ nhật sẽ thay đổi như thế nào khi điểm H tiến gần đến gốc tọa độ? Khi H tiến xa sang phía bên phải thì sao?

Lời giải chi tiết

Hình chữ nhật OHMK có các kích thước lần lượt là hoành độ và tung độ của điểm M.

Ta có điểm M luôn nằm trên đồ thị \(y = \frac{1}{{{x^2}}}\) \((x > 0)\).

Đặt \(M\left( {x;\frac{1}{{{x^2}}}} \right)\) \((x > 0)\)

Khi đó diện tích hình chữ nhật OHMK là: \(\frac{x}{{{x^2}}} = \frac{1}{x}\).

Khi H gần tiến đến gốc tọa độ nghĩa là x dần tiến tới 0 thì diện tích hình chữ nhật sẽ là một số rất lớn.

Khi H tiến xa sang phía bên phải thì x dần tiến tới \( + \infty \) thì diện tích hình chữ nhật sẽ giảm dần về 0.