Giải mục 1 trang 64, 65 SGK Toán 11 tập 1 - Chân trời sáng tạoCho dãy số (left( {{u_n}} right)) với .({u_n} = frac{{{{left( { - 1} right)}^n}}}{n}).
Lựa chọn câu để xem lời giải nhanh hơn
HĐ1 Trả lời câu hỏi Hoạt động 1 trang 64 SGK Toán 11 Chân trời sáng tạo Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{{{\left( { - 1} \right)}^n}}}{n}\). a) Tìm các giá trị còn thiếu trong bảng sau:
b) Với \(n\) thế nào thì \(\left| {{u_n}} \right|\) bé hơn 0,01; 0,001? c) Một số số hạng của dãy số được biểu diễn trên trục số như Hình 1.
Từ các kết quả trên, có nhận xét gì về khoảng cách từ điểm \({u_n}\) đến điểm 0 khi \(n\) trở nên rất lớn? Phương pháp giải: a) Để tìm \(\left| {{u_n}} \right|\), ta thay \(n\) vào công thức \(\left| {{u_n}} \right| = \left| {\frac{{{{\left( { - 1} \right)}^n}}}{n}} \right|\). b) Để tìm \(n\), ta giải các bất đẳng thức \(\left| {{u_n}} \right| < 0,01;\left| {{u_n}} \right| < 0,001\). Lời giải chi tiết: a) \(n = 100 \Leftrightarrow \left| {{u_{100}}} \right| = \left| {\frac{{{{\left( { - 1} \right)}^{100}}}}{{100}}} \right| = \frac{1}{{100}} = 0,01\). \(n = 1000 \Leftrightarrow \left| {{u_{1000}}} \right| = \left| {\frac{{{{\left( { - 1} \right)}^{1000}}}}{{1000}}} \right| = \frac{1}{{1000}} = 0,001\). Như vậy ta có thể điền vào bảng như sau:
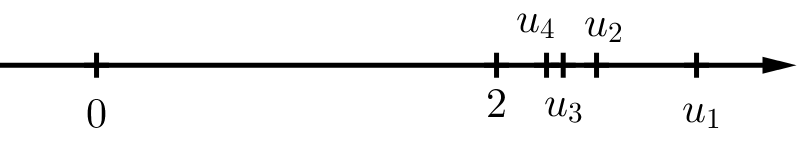
b) \(\left| {{u_n}} \right| < 0,01 \Leftrightarrow \left| {\frac{{{{\left( { - 1} \right)}^n}}}{n}} \right| < 0,01 \Leftrightarrow \frac{1}{n} < 0,01 \Leftrightarrow n > 100\). Vậy \(\left| {{u_n}} \right| < 0,01\) khi \(n > 100\). \(\left| {{u_n}} \right| < 0,001 \Leftrightarrow \left| {\frac{{{{\left( { - 1} \right)}^n}}}{n}} \right| < 0,001 \Leftrightarrow \frac{1}{n} < 0,001 \Leftrightarrow n > 1000\). Vậy \(\left| {{u_n}} \right| < 0,001\) khi \(n > 1000\). c) Dựa vào trục số ta thấy, khoảng cách từ điểm \({u_n}\) đến điểm 0 trở nên rất bé khi \(n\) trở nên rất lớn. TH1 Trả lời câu hỏi Thực hành 1 trang 65 SGK Toán 11 Chân trời sáng tạo Tìm các giới hạn sau: a) \(\lim \frac{1}{{{n^2}}}\); b) \(\lim {\left( { - \frac{3}{4}} \right)^n}\). Phương pháp giải: Áp dụng giới hạn cơ bản: • \(\lim \frac{1}{{{n^k}}} = 0\), với \(k\) nguyên dương bất kì. • \(\lim {q^n} = 0\), với \(q\) là số thực thỏa mãn \(\left| q \right| < 1\). Lời giải chi tiết: a) Áp dụng công thức giới hạn cơ bản với \(k = 2\), ta có: \(\lim \frac{1}{{{n^2}}}\). b) Do \(\left| { - \frac{3}{4}} \right| = \frac{3}{4} < 1\) nên \(\lim {\left( { - \frac{3}{4}} \right)^n} = 0\). HĐ2 Trả lời câu hỏi Hoạt động 2 trang 65 SGK Toán 11 Chân trời sáng tạo Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{2n + 1}}{n}\). a) Cho dãy số \(\left( {{v_n}} \right)\) với \({v_n} = {u_n} - 2\). Tìm giới hạn \(\lim {v_n}\). b) Biểu diễn các điểm \({u_1},{u_2},{u_3},{u_4}\) trên trục số. Có nhận xét gì về vị trí của các điểm \({u_n}\) khi \(n\) trở nên rất lớn? Phương pháp giải: a) Tìm công thức tổng quát của \({v_n}\) sau đó áp dụng giới hạn cơ bản: \(\lim \frac{1}{{{n^k}}} = 0\), với \(k\) nguyên dương bất kì. b) Tính \({u_1},{u_2},{u_3},{u_4}\) rồi biểu diễn trên trục số. Lời giải chi tiết: a) \({v_n} = {u_n} - 2 = \frac{{2n + 1}}{n} - 2 = \frac{{2n + 1 - 2n}}{n} = \frac{1}{n}\). Áp dụng giới hạn cơ bản với \(k = 1\), ta có: \(\lim {v_n} = \lim \frac{1}{n} = 0\). b) \({u_1} = \frac{{2.1 + 1}}{1} = 3,{u_2} = \frac{{2.2 + 1}}{2} = \frac{5}{2},{u_3} = \frac{{2.3 + 1}}{3} = \frac{7}{3},{u_4} = \frac{{2.4 + 1}}{4} = \frac{9}{4}\) Biểu diễn trên trục số:
Nhận xét: Điểm \({u_n}\) càng dần đến điểm 2 khi \(n\) trở nên rất lớn. TH2 Trả lời câu hỏi Thực hành 2 trang 65 SGK Toán 11 Chân trời sáng tạo Tìm các giới hạn sau: a) \(\lim \left( {2 + {{\left( {\frac{2}{3}} \right)}^n}} \right)\); b) \(\lim \left( {\frac{{1 - 4n}}{n}} \right)\). Phương pháp giải: Bước 1: Đặt dãy số cần tính giới hạn là \({u_n}\), từ đó tìm \(a\) sao cho \(\lim \left( {{u_n} - a} \right) = 0\). Bước 2: Áp dụng định lý giới hạn hữu hạn của dãy số: \(\lim {u_n} = a\) nếu \(\lim \left( {{u_n} - a} \right) = 0\). Lời giải chi tiết: a) Đặt \({u_n} = 2 + {\left( {\frac{2}{3}} \right)^n} \Leftrightarrow {u_n} - 2 = {\left( {\frac{2}{3}} \right)^n}\). Suy ra \(\lim \left( {{u_n} - 2} \right) = \lim {\left( {\frac{2}{3}} \right)^n} = 0\). Theo định nghĩa, ta có \(\lim {u_n} = 2\). Vậy \(\lim \left( {2 + {{\left( {\frac{2}{3}} \right)}^n}} \right) = 2\). b) Đặt \({u_n} = \frac{{1 - 4n}}{n} = \frac{1}{n} - 4 \Leftrightarrow {u_n} - \left( { - 4} \right) = \frac{1}{n}\). Suy ra \(\lim \left( {{u_n} - \left( { - 4} \right)} \right) = \lim \frac{1}{n} = 0\). Theo định nghĩa, ta có \(\lim {u_n} = - 4\). Vậy \(\lim \left( {\frac{{1 - 4n}}{n}} \right) = - 4\).
|