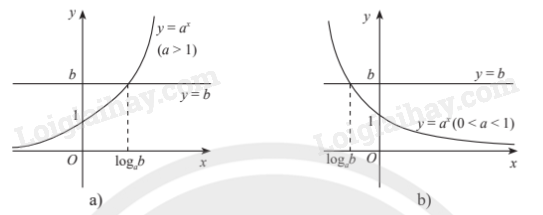
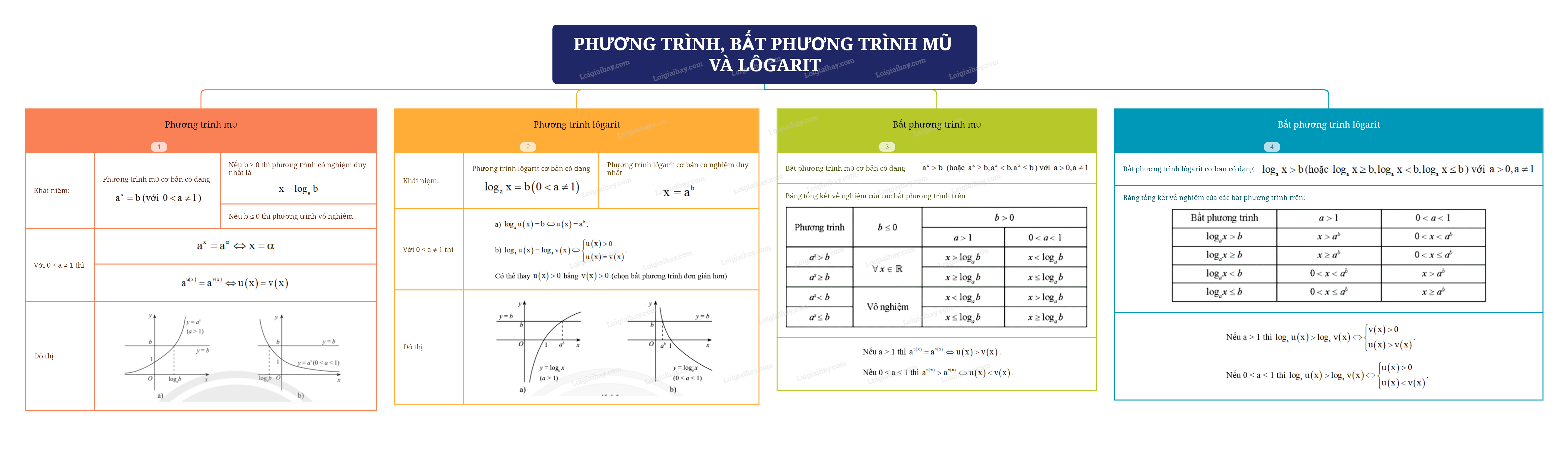
Lý thuyết Phương trình, bất phương trình mũ và lôgarit - Toán 11 Chân trời sáng tạo

1. Phương trình mũ cơ bản

Phương trình mũ cơ bản có dạng ${a^x} = b$(với $a > 0,a \ne 1$).

- Nếu b > 0 thì phương trình có nghiệm duy nhất $x = {\log _a}b$.

- Nếu b $\le$ 0 thì phương trình vô nghiệm.

Chú ý: Với $a > 0,a \ne 1$

a) ${a^x} = {a^\alpha } \Leftrightarrow x = \alpha$.

b) Tổng quát hơn, ${a^{u\left( x \right)}} = {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) = v\left( x \right)$

Minh họa bằng đồ thị:

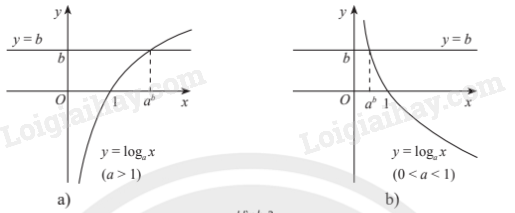
2. Phương trình lôgarit cơ bản

Phương trình lôgarit cơ bản có dạng ${\log _a}x = b\left( {a > 0,a \ne 1} \right)$.

Phương trình luôn có nghiệm duy nhất $x = {a^b}$.

Chú ý: Với $a > 0,a \ne 1$

a) ${\log _a}u\left( x \right) = b \Leftrightarrow u\left( x \right) = {a^b}$.

b) ${\log _a}u\left( x \right) = {\log _a}v\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}u\left( x \right) > 0\\u\left( x \right) = v\left( x \right)\end{array} \right.$.

Có thể thay $u\left( x \right) > 0$ bằng $v\left( x \right) > 0$ (chọn bất phương trình đơn giản hơn)

Minh họa bằng đồ thị:

3. Bất phương trình mũ cơ bản

Bất phương trình mũ cơ bản có dạng ${a^x} > b$ (hoặc ${a^x} \ge b,{a^x} < b,{a^x} \le b$) với $a > 0,a \ne 1$.

Bảng tổng kết về nghiệm của các bất phương trình trên:

Chú ý:

Nếu a > 1 thì ${a^{u\left( x \right)}} = {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) > v\left( x \right)$.

Nếu 0 < a < 1 thì ${a^{u\left( x \right)}} > {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) < v\left( x \right)$.

4. Bất phương trình lôgarit cơ bản

Bất phương trình lôgarit cơ bản có dạng ${\log _a}x > b$(hoặc ${\log _a}x \ge b,{\log _a}x < b,{\log _a}x \le b$) với $a > 0,a \ne 1$.

Bảng tổng kết về nghiệm của các bất phương trình trên:

Chú ý:

Nếu a > 1 thì ${\log _a}u\left( x \right) > {\log _a}v\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}v\left( x \right) > 0\\u\left( x \right) > v\left( x \right)\end{array} \right.$.

Nếu 0 < a < 1 thì ${\log _a}u\left( x \right) > {\log _a}v\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}u\left( x \right) > 0\\u\left( x \right) < v\left( x \right)\end{array} \right.$.