Trắc nghiệm Bài 1: Tổng ba góc của một tam giác Toán 7 Cánh diềuĐề bài
Câu 2 :
Khẳng định nào sau đây là sai?
Câu 3 :
Tam giác ABC có \(\widehat B + \widehat C = \widehat A\) và \(\widehat C = 2\widehat B\). Tia phân giác của góc C cắt AB ở D. Tính \(\widehat {ADC}\)
Câu 4 :
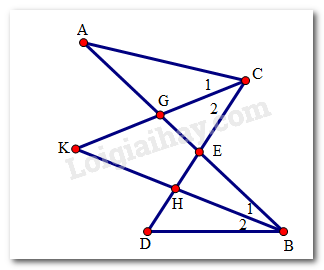
Cho hai đoạn thẳng AB và CD cắt nhau ở E. Các tia phân giác của các góc ACE và DBE cắt nhau ở K. Tính số đo góc BKC?
Câu 6 :
Tam giác ABC có \(\widehat A = {80^0},\widehat B - \widehat C = {50^0}\). Số đo góc B và góc C lần lượt là:
Câu 7 :
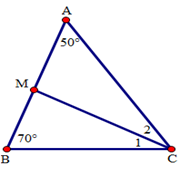
Cho tam giác ABC có \(\widehat A = {50^0},\widehat B = {70^0}\). Tia phân giác của góc C cắt cạnh AB tại M. Số đo góc BMC là:
Câu 9 :
Cho tam giác ABC có \(\widehat A = 86^\circ ;\widehat B = 62^\circ \). Số đo góc C là:
Lời giải và đáp án
Đáp án : D Phương pháp giải :
Góc ngoài tam giác bằng tổng 2 góc trong không kề với nó. Lời giải chi tiết :
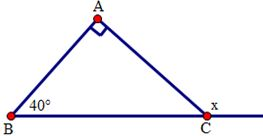
Ta có góc cần tính là góc ngoài tại đỉnh C của tam giác ABC nên: \(x = \widehat A + \widehat B = 90^\circ + 40^\circ = 130^\circ \)
Câu 2 :
Khẳng định nào sau đây là sai?
Đáp án : C Phương pháp giải :
Lý thuyết về 3 loại tam giác: Tam giác tù, tam giác vuông, tam giác nhọn Lời giải chi tiết :
Các khẳng định A,B,D đúng. Khẳng định C sai vì: Góc lớn nhất trong tam giác nhọn là một góc nhọn, góc lớn nhất trong tam giác vuông là góc vuông. Do đó không thể khẳng định góc lớn nhất trong tam giác là góc tù.
Câu 3 :
Tam giác ABC có \(\widehat B + \widehat C = \widehat A\) và \(\widehat C = 2\widehat B\). Tia phân giác của góc C cắt AB ở D. Tính \(\widehat {ADC}\)
Đáp án : A Phương pháp giải :
Sử dụng tính chất tổng các góc của một tam giác, tính chất tia phân giác của một góc Lời giải chi tiết :
Xét tam giác ABC có \(\widehat A + \widehat B + \widehat C = {180^0}\) mà \(\widehat B + \widehat C = \widehat A\), do đó \(2\widehat A = {180^0} \Rightarrow \widehat A = {90^0}\). Trong tam giác ABC do \(\widehat A = {90^0}\) nên \(\widehat B + \widehat C = {90^ \circ }\). Mà \(\widehat C = 2\widehat B\) do đó \(3\widehat B = {90^0} \Rightarrow \widehat B = {30^0}\)nên \(\widehat C = {60^0}\) Do CD là tia phân giác của góc ACD nên \(\widehat {ACD} = \widehat {DCB} = \widehat C:2 = {60^ \circ }:2 = {30^ \circ }\) Xét tam giác ADC có: \(\widehat A + \widehat {ADC} + \widehat {ACD} = {180^0} \Rightarrow \widehat {ADC} = {180^0} - \left( {\widehat A + \widehat {ACD}} \right) = {180^0} - \left( {{{30}^0} + {{90}^ \circ }} \right) = {60^ \circ }\)
Câu 4 :
Cho hai đoạn thẳng AB và CD cắt nhau ở E. Các tia phân giác của các góc ACE và DBE cắt nhau ở K. Tính số đo góc BKC?
Đáp án : C Phương pháp giải :
Áp dụng tính chất tổng ba góc của một tam giác Lời giải chi tiết :
Gọi G là giao điểm của CK và AE, H là giao điểm của BK và DE. Xét tam giác KGB và tam giác AGC và theo tính chất góc ngoài của tam giác ta có:\(\left\{ \begin{array}{l}\widehat K + \widehat {{B_1}} = \widehat {AGK}\\\widehat A + \widehat {{C_1}} = \widehat {AGK}\end{array} \right. \Rightarrow \widehat K + \widehat {{B_1}} = \widehat A + \widehat {{C_1}}\) (1) Xét tam giác KHC và tam giác DHB và theo tính chất góc ngoài của tam giác ta có:\(\left\{ \begin{array}{l}\widehat K + \widehat {{C_2}} = \widehat {EHB}\\\widehat D + \widehat {{B_2}} = \widehat {EHB}\end{array} \right. \Rightarrow \widehat K + \widehat {{C_2}} = \widehat D + \widehat {{B_2}}\) (2) Do \(\widehat {{B_1}} = \widehat {{B_2}}\) (BK là tia phân giác của góc DBA); \(\widehat {{C_1}} = \widehat {{C_2}}\) ( CK là tia phân giác của góc ACD). Nên cộng (1) với (2) ta được \(2\widehat K = \widehat A + \widehat D\), do đó \(\widehat K = \frac{{\widehat A + \widehat D}}{2}\) hay \(\widehat {BKC} = \frac{{\widehat {BAC} + \widehat {BDC}}}{2}\)
Đáp án : C Phương pháp giải :
Áp dụng tính chất tổng ba góc của một tam giác Lời giải chi tiết :
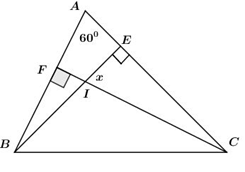
Áp dụng tính chất tổng ba góc trong tam giác ACF có :\(\widehat A + \widehat {ACF} + \widehat {AFC} = {180^0} \Leftrightarrow {60^0} + \widehat {ACF} + {90^0} = {180^0}\) \( \Rightarrow \widehat {ACF} = {180^0} - {60^0} - {90^0} = {30^0}.\) Áp dụng tính chất tổng ba góc trong \(\Delta IEC\) ta có: \(\widehat {IEC} + \widehat {ECI} + \widehat {EIC} = {180^0} \Leftrightarrow {30^0} + x + {90^0} = {180^0}\) \( \Rightarrow x = {180^0} - {30^0} - {90^0} = {60^0}.\)
Câu 6 :
Tam giác ABC có \(\widehat A = {80^0},\widehat B - \widehat C = {50^0}\). Số đo góc B và góc C lần lượt là:
Đáp án : B Phương pháp giải :
+ Áp dụng tính chất tổng ba góc của một tam giác, tính tổng 2 góc B và C + Bài toán trở về tìm 2 số biết tổng và hiệu của chúng Lời giải chi tiết :
Áp dụng định lí tổng ba góc trong tam giác ABC, ta có: \(\widehat A + \widehat B + \widehat C = 180^\circ \Rightarrow \widehat B + \widehat C = 180^\circ - 80^\circ = 100^\circ \) Ta có: \(\begin{array}{l}\widehat C = (100^\circ - 50^\circ ):2 = 25^\circ ;\\\widehat B = \widehat C + 50^\circ = 25^\circ + 50^\circ = 75^\circ \end{array}\)
Câu 7 :
Cho tam giác ABC có \(\widehat A = {50^0},\widehat B = {70^0}\). Tia phân giác của góc C cắt cạnh AB tại M. Số đo góc BMC là:
Đáp án : B Phương pháp giải :
Áp dụng tính chất tổng ba góc của một tam giác, tính chất tia phân giác của một góc. Lời giải chi tiết :
Áp dụng định lí tổng ba góc trong tam giác ABC, ta có: \(\widehat A + \widehat B + \widehat C = {180^0}\) suy ra \(\widehat C = {180^0} - \left( {\widehat A + \widehat B} \right) \) \(= {180^0} - \left( {{{50}^0} + {{70}^0}} \right) = {60^0}\). Do CM là tia phân giác của góc ACB nên \(\widehat {{C_1}} = \widehat {{C_2}} = \frac{{\widehat C}}{2} = \frac{{{{60}^0}}}{2} = {30^0}\). Áp dụng định lí tổng ba góc trong tam giác BMC có: \(\widehat B + \widehat {BMC} + {\widehat C_1} = {180^0} \) suy ra \(\widehat {BMC} = {180^0} - \left( {\widehat B + \widehat {{C_1}}} \right) \) \(= {180^0} - \left( {{{70}^0} + {{30}^0}} \right) = {80^0}\)
Đáp án : B Phương pháp giải :
Áp dụng tính chất tổng ba góc của một tam giác: Trong \(\Delta ABC:\,\widehat A + \widehat B + \widehat C = {180^0}.\) Lời giải chi tiết :
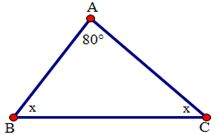
Áp dụng tính chất tổng ba góc trong tam giác ABC, ta có: \(\widehat A + \widehat B + \widehat C = {180^0}\) Suy ra \(\widehat B + \widehat C = {180^0} - \widehat A = {180^0} - {80^0} = {100^0}\). Hay \(x + x = {100^0}\) hay \( 2x = {100^0} \) suy ra \( x = {50^0}\)
Câu 9 :
Cho tam giác ABC có \(\widehat A = 86^\circ ;\widehat B = 62^\circ \). Số đo góc C là:
Đáp án : A Phương pháp giải :
Tổng số đo 3 góc trong 1 tam giác bằng 180 độ Lời giải chi tiết :
Áp dụng định lí tổng ba góc trong tam giác ABC, ta có: \(\begin{array}{l}\widehat A + \widehat B + \widehat C = 180^\circ \\ \Rightarrow 86^\circ + 62^\circ + \widehat C = 180^\circ \\ \Rightarrow \widehat C = 180^\circ - 86^\circ - 62^\circ = 32^\circ \end{array}\)
Đáp án : B Phương pháp giải :
Tổng số đo 3 góc trong 1 tam giác bằng 180 độ Lời giải chi tiết :
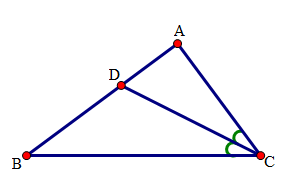
Áp dụng định lí tổng số đo 3 góc trong 3 tam giác ABD, ACD và ABC, ta được: \(\widehat {BAD} + \widehat {ABD} + \widehat {ADB} = 180^\circ \) \(\widehat {CAD} + \widehat {ADC} + \widehat {ACB} = 180^\circ \) \(\widehat {BAC} + \widehat {ACD} + \widehat {ABD} = 180^\circ \) Vậy A,C,D đúng
|
