Giải mục 2 trang 76 SGK Toán 11 tập 2 - Chân trời sáng tạo

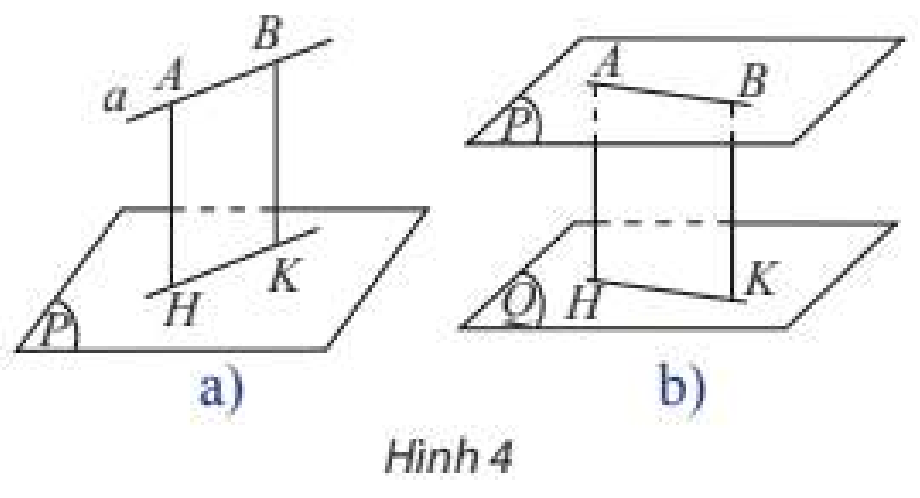
Hoạt động 2

a) Cho đường thẳng $a$ song song với mặt phẳng $\left( P \right)$. Lấy hai điểm $A,B$ tuỳ ý trên $a$ và gọi $H,K$ lần lượt là hình chiếu vuông góc của $A$ và $B$ trên $\left( P \right)$ (Hình 4a). So sánh độ dài hai đoạn thẳng $AH$ và $BK$.

b) Cho hai mặt phẳng song song $\left( P \right)$ và $\left( Q \right)$. Lấy hai điểm $A,B$ tuỳ ý trên $\left( P \right)$ và gọi $H,K$ lần lượt là hình chiếu vuông góc của $A$ và $B$ trên $\left( Q \right)$ (Hình 4b). So sánh độ dài hai đoạn thẳng $AH$ và $BK$.

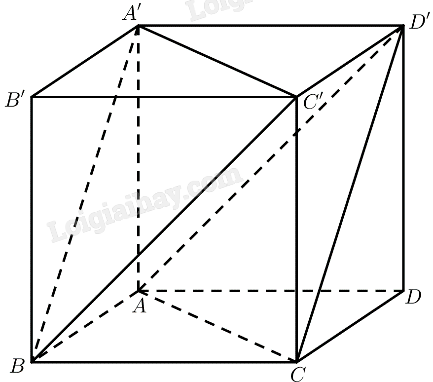
Phương pháp giải:

Sử dụng tính chất của phép chiếu vuông góc.

Lời giải chi tiết:

a) Ta có:

$\left. \begin{array}{l}AH \bot \left( P \right)\\BK \bot \left( P \right)\end{array} \right\} \Rightarrow AH\parallel BK$

Mà $AB\parallel HK$

$\Rightarrow ABKH$ là hình bình hành có $AH \bot \left( P \right) \Rightarrow AH \bot HK \Rightarrow \widehat {AHK} = {90^ \circ }$

Vậy $ABKH$ là hình chữ nhật.

Vậy $AH = BK$.

b) Ta có:

$\left. \begin{array}{l}AH \bot \left( Q \right)\\BK \bot \left( Q \right)\end{array} \right\} \Rightarrow AH\parallel BK$

Mà $AB\parallel HK$

$\Rightarrow ABKH$ là hình bình hành có $AH \bot \left( Q \right) \Rightarrow AH \bot HK \Rightarrow \widehat {AHK} = {90^ \circ }$

Vậy $ABKH$ là hình chữ nhật.

Vậy $AH = BK$.

Quảng cáo

Thực hành 2

Cho hình lập phương $ABCD.A'B'C'D'$ có cạnh bằng $a$. Tính khoảng cách:

a) Giữa hai mặt phẳng $\left( {ACD'} \right)$ và $\left( {A'C'B} \right)$.

b) Giữa đường thẳng $AB$ và $\left( {A'B'C'D'} \right)$.

Phương pháp giải:

‒ Cách tính góc giữa hai mặt phẳng: Góc giữa hai mặt phẳng $\left( \alpha  \right)$ và $\left( \beta  \right)$ là góc giữa hai đường thẳng lần lượt vuông góc với $\left( \alpha  \right)$ và $\left( \beta  \right)$.

‒ Cách tính góc giữa đường thẳng và mặt phẳng: ta tính góc giữa đường thẳng và hình chiếu của nó lên mặt phẳng.

Lời giải chi tiết:

a) $AA'C'C$ là hình chữ nhật

$\left. \begin{array}{l} \Rightarrow AC\parallel A'C'\\A'C' \subset \left( {A'C'B} \right)\end{array} \right\} \Rightarrow AC\parallel \left( {A'C'B} \right)$

$ABC'D'$ là hình bình hành

$\left. \begin{array}{l} \Rightarrow AD'\parallel BC'\\BC' \subset \left( {A'C'B} \right)\end{array} \right\} \Rightarrow AD'\parallel \left( {A'C'B} \right)$

Ta có:

$\left. \begin{array}{l}AC\parallel \left( {A'C'B} \right)\\AD'\parallel \left( {A'C'B} \right)\\AC,A{\rm{D}}' \subset \left( {AC{\rm{D}}'} \right)\end{array} \right\} \Rightarrow \left( {AC{\rm{D}}'} \right)\parallel \left( {A'C'B} \right) \Rightarrow \left( {\left( {AC{\rm{D}}'} \right),\left( {A'C'B} \right)} \right) = {0^ \circ }$

b) Ta có:

$\left. \begin{array}{l}AB\parallel A'B'\\A'B' \subset \left( {A'B'C'D'} \right)\end{array} \right\} \Rightarrow AB\parallel \left( {A'B'C'D'} \right) \Rightarrow \left( {AB,\left( {A'B'C'D'} \right)} \right) = {0^ \circ }$