Bài tập trắc nghiệm Toán 7 - Kết nối tri thức

Trắc nghiệm Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác Toán 7 Kết nối tri thức

Đề bài

Câu 1 :

Cho tam giác $BAC$ và tam giác $KEF$ có $BA = EK,$ $\widehat A = \widehat K$ , $CA = KF.$ Phát biểu nào trong trong các phát biểu sau đây là đúng:

A

$\Delta BAC = \Delta EKF$
B

$\Delta BAC = \Delta EFK$
C

$\Delta {\rm A}BC = \Delta FKE$
D

$\Delta BAC = \Delta KEF$

Câu 2 :

Cho tam giác $ABC$ và tam giác $MNP$ có $\widehat A = \widehat {M,}\widehat B = \widehat N$ . Cần thêm điều kiện gì để tam giác $ABC$ và tam giác $MNP$ bằng nhau theo trường hợp góc – cạnh – góc:

A

$AC = MP$
B

$AB = MN$
C

$BC = NP$
D

$AC = MN$

Câu 3 :

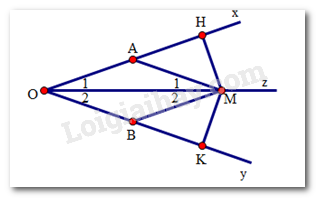
Cho góc nhọn $xOy,Oz$ là tia phân giác của góc đó. Qua điểm $A$ thuộc tia $Ox$ kẻ đường thẳng song song với $Oy$ cắt $Oz$ ở $M.$ Qua $M$ kẻ đường thẳng song song với $Ox$ cắt $Oy$ ở $B.$ Chọn câu đúng.

A

$OA > OB;MA > MB$
B

$OA = OB;MA = MB$
C

$OA < OB;MA < MB$
D

$OA < OB;MA = MB$

Câu 4 :

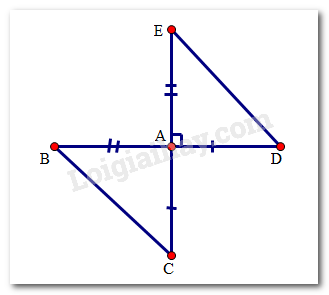
Cho hai đoạn thẳng $BD$ và $EC$ vuông góc với nhau tại $A$ sao cho $AB = AE,AD = AC,AB < AC.$ Phát biểu nào trong các phát biểu sau đây là sai:

A

$\Delta AED = \Delta ABC$
B

$BC = ED$
C

$EB = CD$
D

$\widehat {ABC} = \widehat {AED}$ .

Câu 5 :

Cho góc nhọn $xOy.$ Trên tia $Ox$ lấy hai điểm $A,C,$ trên tia $Oy$ lấy hai điểm $B,D$ sao cho $OA = OB,OC = OD$ ( $A$ nằm giữa $O$ và $C,$ $B$ nằm giữa $O$ và $D$ ). So sánh hai góc $\widehat {CAD}$ và $\widehat {CBD}.$

A

$\widehat {CBD} = \widehat {CAD}$
B

$\widehat {CBD} < \widehat {CAD}$
C

$\widehat {CBD} > \widehat {CAD}$
D

$2.\widehat {CBD} = \widehat {CAD}$

Câu 6 :

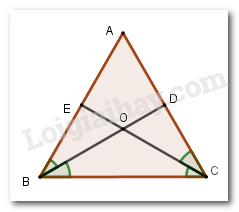
Cho tam giác $ABC$ có $AB = AC = BC,$ phân giác $BD$ và $CE$ cắt nhau tại $O.$ Tính $\widehat {BOC}.$

A

${60^0}$
B

${80^0}$
C

$120^\circ$
D

${100^0}$

Câu 7 :

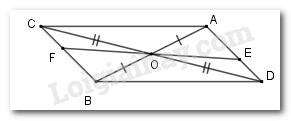
Cho hai đoạn thẳng $AB$ và $CD$ cắt nhau tại $O$ là trung điểm của mỗi đoạn thẳng đó. Lấy $E;\,F$ lần lượt là điểm thuộc đoạn $AD$ và $BC$ sao cho $AE = BF.$ Cho $OE = 2cm$ , tính $EF.$

A

$4\,cm$
B

$2cm$
C

$3\,cm$
D

$3,5\,cm$

Câu 8 :

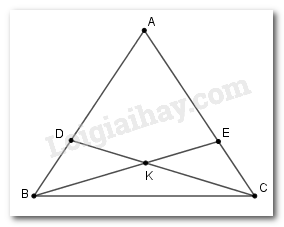
Cho tam giác $ABC$ có $AB = AC.$ Trên các cạnh $AB$ và $AC$ lấy các điểm $D,E$ sao cho $AD = AE.$ Gọi $K$ là giao điểm của $BE$ và $CD$ . Chọn câu sai.

A

$BE = CD$
B

$BK = KC$
C

$BD = CE$
D

$DK = KC$

Câu 9 :

Cho tam giác $DEF$ và tam giác $HKG$ có $\widehat D = \widehat H$ , $\widehat E = \widehat K$ , $DE = HK.$ Biết $\widehat F = {80^0}$ . Số đo góc $G$ là:

A

${70^0}$
B

${80^0}$
C

${90^0}$
D

${100^0}$

Câu 10 :

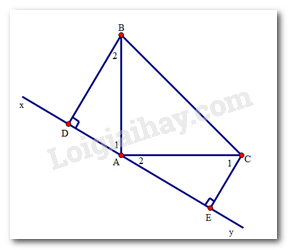
Cho tam giác $ABC$ vuông tại $A$ có $AB = AC.$ Qua $A$ kẻ đường thẳng $xy$ sao cho $B,C$ nằm cùng phía với $xy.$ Kẻ $BD$ và $CE$ vuông góc với $xy.$ Chọn câu đúng.

A

$DE = BD + CE$
B

$DE = BD - CE$
C

$CE = BD + DE$
D

$CE = BD - DE$

Cho tam giác $ABC$ vuông tại $A.$ Tia phân giác của góc $ABC$ cắt $AC$ tại $D,$ lấy $E$ trên cạnh $BC$ sao cho $BE = AB.$

Câu 11

Chọn câu đúng.

A.

$\Delta ABD{\rm{ }} = \Delta EBD$
B.

$\Delta ABD{\rm{ }} = \Delta BED$
C.

$DC = DE$
D.

$\Delta ABD = \Delta CBD$

Câu 12

Trên tia đối của tia $DE$ lấy điểm $M$ sao cho $DM = DC$ . So sánh $EC$ và $AM$ .

A.

$EC < AM$
B.

$EC = AM$
C.

$EC > AM$
D.

Chưa đủ điều kiện để so sánh

Câu 13

Trên tia đối của tia $DE$ lấy điểm $M$ sao cho $DM = DC$ . Nối $AE,$ so sánh số đo $\widehat {AEC};\widehat {EAM}$ .

A.

$\widehat {AEC} > \widehat {EAM}$
B.

$\widehat {AEC} < \widehat {EAM}$
C.

$\widehat {AEC} = \widehat {EAM}$
D.

Chưa đủ điều kiện so sánh

Cho điểm $A$ nằm trong góc nhọn $xOy.$ Vẽ $AH$ vuông góc với $Ox,$ trên tia đối của tia $HA$ lấy điểm $B$ sao cho $HB = HA.$ Vẽ $AK$ vuông góc với $Oy,$ trên tia đổi của tia $KA$ lấy điểm $C$ sao cho $KC = KA.$

Câu 14

So sánh $OB;OC$ .

A.

$OB < OC$
B.

$OB = OC$
C.

$OB > OC$
D.

$OB \ge OC$

Câu 15

Biết $\widehat {xOy} = \alpha .$ Tính $\widehat {BOC}.$

A.

$3\alpha$
B.

$4\alpha$
C.

$2\alpha$
D.

$\alpha$

Câu 16 :

A

$4\,cm$
B

$2cm$
C

$3\,cm$
D

$3,5\,cm$

Câu 17 :

Cho tam giác $ABC$ có $M,N$ lần lượt là trung điểm của $AB,AC.$ Trên tia đối của tia $MC$ lấy $D$ sao cho $MD = MC$ . Trên tia đối của tia $NB$ lấy điểm $E$ sao cho $NE = NB.$

(I) $\Delta AMD = \Delta BMC$

(II) $\Delta ANE = \Delta CNB$

(III) $A,D,E$ thẳng hàng

(IV) $A$ là trung điểm của đoạn thẳng $DE$

Số khẳng định đúng trong các khẳng định trên là

A

$0$
B

$2$
C

$4$
D

$3$

Cho góc nhọn $xOy$ và $Oz$ là tia phân giác của góc đó. Trên tia $Ox$ lấy điểm $A$ và trên tia $Oy$ lấy điểm $B$ sao cho $OA = OB.$ Gọi $C$ là một điểm bất kỳ trên tia $Oz.$

Câu 18

Chọn câu sai.

A.

$AC = OB$
B.

$AC = BC$
C.

$\widehat {OAC} = \widehat {OBC}$
D.

$CO$ là tia phân giác của $\widehat {BCA}.$

Câu 19

Gọi $I$ là giao của $AB$ và $Oz.$ Tính góc $AIC.$

A.

$120^\circ$
B.

$90^\circ$
C.

$60^\circ$
D.

${100^0}$

Cho tam giác $ABC$ có $AB = AC = BC,$ phân giác $BD$ và $CE$ cắt nhau tại $O.$

Câu 20

Chọn câu đúng.

A.

$CE \bot \;AB$
B.

$BD\; \bot AC$
C.

$DC = BC$
D.

Cả A, B đều đúng.

Câu 21

Tính $\widehat {BOC}.$

A.

${60^0}$
B.

${80^0}$
C.

$120^\circ$
D.

${100^0}$

Câu 22 :

Cho đoạn thẳng $AB$ , trên đường trung trực $d$ của đoạn $AB$ lấy điểm $M.$ So sánh $AM$ và $BM.$

A

$MA = MB$
B

$MA > MB$
C

$MA < MB$
D

$2.MA = MB$

Câu 23 :

Cho tam giác $ABC$ có $\widehat A = {90^0}$ , tia phân giác $BD$ của góc $B$ ( $D \in AC$ ). Trên cạnh $BC$ lấy điểm $E$ sao cho $BE = BA.$ Hai góc nào sau đây bằng nhau?

A

$\widehat {EDC};\widehat {BAC}$
B

$\widehat {EDC};\widehat {ACB}$
C

$\widehat {EDC};\widehat {ABC}$
D

$\widehat {EDC};\widehat {EC{\rm{D}}}$

Câu 24 :

Cho tam giác $DEF$ và tam giác $HKG$ có $DE = HK$ , $\widehat E = \widehat K$ , $EF = KG.$ Biết $\widehat D = {70^0}$ . Số đo góc $H$ là:

A

${70^0}$
B

${80^0}$
C

${90^0}$
D

${100^0}$

Cho góc nhọn $xOy.$ Trên tia $Ox$ lấy hai điểm $A,C,$ trên tia $Oy$ lấy hai điểm $B,D$ sao cho $OA = OB,OC = OD$ ( $A$ nằm giữa $O$ và $C,$ $B$ nằm giữa $O$ và $D$ ).

Câu 25

Chọn câu đúng.

A.

$\Delta OAD = \Delta OCB$
B.

$\Delta ODA = \Delta OBC$
C.

$\Delta AOD = \Delta BCO$
D.

$\Delta OAD = \Delta OBC$ .

Câu 26

So sánh hai góc $\widehat {CAD}$ và $\widehat {CBD}.$

A.

$\widehat {CBD} = \widehat {CAD}$
B.

$\widehat {CBD} < \widehat {CAD}$
C.

$\widehat {CBD} > \widehat {CAD}$
D.

$\widehat {CBD} =2.\widehat {CAD}$ .

Câu 27 :

Cho tam giác $BAC$ và tam giác $KEF$ có $BA = EK,$ $\widehat A = \widehat K$ , $CA = KF.$ Phát biểu nào trong trong các phát biểu sau đây là đúng:

A

$\Delta BAC = \Delta EKF$
B

$\Delta BAC = \Delta EFK$
C

$\Delta {\rm A}BC = \Delta FKE$
D

$\Delta BAC = \Delta KEF$

Câu 28 :

Cho tam giác $ABC$ và tam giác $MHK$ có: $AB = MH$ , $\widehat A = \widehat M$ . Cần thêm một điều kiện gì để hai tam giác $ABC$ và $MHK$ bằng nhau theo trường hợp cạnh – góc – cạnh:

A

$BC = MK$
B

$BC = HK$
C

$AC = MK$
D

$AC = HK$

Câu 29 :

Cho tam giác $ABC$ và tam giác $NPM$ có $BC = PM;\,\widehat B = \widehat P$ . Cần thêm một điều kiện gì để tam giác $MPN$ và tam giác $CBA$ bằng nhau theo trường hợp góc – cạnh – góc ?

A

$\widehat M = \widehat A$
B

$\widehat A = \widehat P$
C

$\widehat C = \widehat M$
D

$\widehat A = \widehat N$

Câu 30 :

Cho tam giác $ABC$ và tam giác $MNP$ có $\widehat B = \widehat N = {90^ \circ }$ , $AC = MP,$ $\widehat C = \widehat M$ . Phát biểu nào trong các phát biểu sau đây là đúng:

A

$\Delta ABC = \Delta PMN$
B

$\Delta ACB = \Delta PNM$
C

$\Delta BAC = \Delta MNP$
D

$\Delta ABC = \Delta PNM$

Câu 31 :

Cho tam giác $DEF$ và tam giác $HKG$ có $\widehat D = \widehat H$ , $\widehat E = \widehat K$ , $DE = HK.$ Biết $\widehat F = {80^0}$ . Số đo góc $G$ là:

A

${70^0}$
B

${80^0}$
C

${90^0}$
D

${100^0}$

Câu 32 :

Cho tam giác $ABC$ và tam giác $DEF$ có $AB = DE,$ $\widehat B = \widehat E$ , $\widehat A = \widehat D$ . Biết $AC = 6cm.$ Độ dài $DF$ là:

A

$4cm\;\;\;\;$
B

$5cm$
C

$6cm\;\;\;\;$
D

$7cm$

Câu 33 :

Cho tam giác $ABC$ vuông tại $A$ có $AB = AC.$ Qua $A$ kẻ đường thẳng $xy$ sao cho $B,C$ nằm cùng phía với $xy.$ Kẻ $BD$ và $CE$ vuông góc với $xy.$ Chọn câu đúng.

A

$DE = BD + CE$
B

$DE = BD - CE$
C

$CE = BD + DE$
D

$CE = BD - DE$

Câu 34 :

Cho tam giác $ABC,D$ là trung điểm của $AB.$ Đường thẳng qua $D$ và song song với $BC$ cắt $AC$ ở $E,$ đường thẳng qua $E$ và song song với $AB$ cắt $BC$ ở $F.$ Khi đó

A

$\Delta ADE = \Delta EFC$
B

$\Delta ADE = \Delta DBF$
C

$\Delta EFC = \Delta DBF$
D

Cả A, B, C đều đúng.

Câu 35 :

Cho tam giác $ABC$ có $\widehat A = {60^0}.$ Tia phân giác của góc $B$ cắt $AC$ ở $D,$ tia phân giác của góc $C$ cắt $AB$ ở $E.$ Các tia phân giác đó cắt nhau ở $I.$ Tính độ dài $ID,$ biết $IE = 2cm.$

A

$ID = 4cm$
B

$ID = 2cm$
C

$ID = 8cm$
D

$ID = 3cm$

Câu 36 :

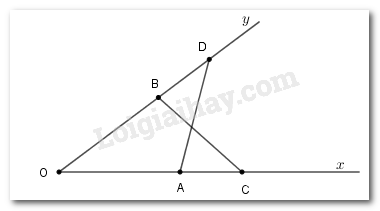
Cho hai đoạn thẳng $AB,CD$ song song với nhau. Hai đoạn thẳng này chắn giữa hai đường thẳng song song $AC,BD$ . Chọn câu đúng:

A

$AB = CD$
B

$AB > CD$
C

$AB < CD$
D

$AC > BD$

Lời giải và đáp án

Câu 1 :

Cho tam giác $BAC$ và tam giác $KEF$ có $BA = EK,$ $\widehat A = \widehat K$ , $CA = KF.$ Phát biểu nào trong trong các phát biểu sau đây là đúng:

A

$\Delta BAC = \Delta EKF$
B

$\Delta BAC = \Delta EFK$
C

$\Delta {\rm A}BC = \Delta FKE$
D

$\Delta BAC = \Delta KEF$

Đáp án : A

Phương pháp giải :

Sử dụng trường hợp bằng nhau thứ hai của tam giác

Lời giải chi tiết :

Xét tam giác $BAC$ và tam giác $KEF$ có $BA = EK,$ $\widehat A = \widehat K$ , $CA = KF.$ suy ra $\Delta BAC = \Delta EKF$ (c.g.c).

Chú ý

Ta cần viết đúng thứ tự đỉnh tương ứng của hai tam giác bằng nhau

Câu 2 :

A

$AC = MP$
B

$AB = MN$
C

$BC = NP$
D

$AC = MN$

Đáp án : B

Phương pháp giải :

Áp dụng trường hợp bằng nhau thứ ba của tam giác.

Lời giải chi tiết :

Ta thấy hai tam giác $ABC$ và tam giác $MNP$ có hai yếu tố về góc $\widehat A = \widehat {M,}\widehat B = \widehat N$ .

Để tam giác $ABC$ và tam giác $MNP$ bằng nhau theo trường hợp góc – cạnh – góc thì cần thêm điều kiện về cạnh kề hai góc đã cho đó là $AB = MN.$

Câu 3 :

A

$OA > OB;MA > MB$
B

$OA = OB;MA = MB$
C

$OA < OB;MA < MB$
D

$OA < OB;MA = MB$

Đáp án : B

Phương pháp giải :

+ Từ tính chất đường thẳng song song, tính chất tia phân giác suy ra các cặp góc bằng nhau.

+ Dựa vào trường hợp bằng nhau thứ ba của tam giác và hệ quả của trường hợp bằng nhau thứ ba để chứng minh các tam giác bằng nhau để suy ra các cặp cạnh bằng nhau.

Lời giải chi tiết :

Ta có:

$\widehat {{M_1}} = \widehat {{O_2}}$ (hai góc so le trong)

$\widehat {{M_2}} = \widehat {{O_1}}$ (hai góc so le trong)

$\widehat {{O_2}} = \widehat {{O_1}}$ (do Oz là tia phân giác của góc xOy)

Do đó $\widehat {{M_2}} = \widehat {{M_1}}$

Xét tam giác $AOM$ và tam giác $BOM$ có:

$\widehat {{M_2}} = \widehat {{M_1}}$ (cmt)

$OM$ là cạnh chung

$\widehat {{O_2}} = \widehat {{O_1}}$ (cmt)

$\Rightarrow \Delta AOM = \Delta BOM(g.c.g)$

Do đó $OA = OB;MA = MB$ (các cặp cạnh tương ứng).

Câu 4 :

Cho hai đoạn thẳng $BD$ và $EC$ vuông góc với nhau tại $A$ sao cho $AB = AE,AD = AC,AB < AC.$ Phát biểu nào trong các phát biểu sau đây là sai:

A

$\Delta AED = \Delta ABC$
B

$BC = ED$
C

$EB = CD$
D

$\widehat {ABC} = \widehat {AED}$ .

Đáp án : C

Phương pháp giải :

+ Sử dụng trường hợp bằng nhau thứ hai của tam giác để chứng minh hai tam giác bằng nhau.

+ Sử dụng tính chất của hai tam giác bằng nhau để suy ra các tính chất về cạnh, về góc tương ứng.

Lời giải chi tiết :

Xét hai tam giác $ABC$ và tam giác $AED$ có:

$AB = AB;$ $\widehat {BAD} = \widehat {BAC}$ (hai góc đối đỉnh); $AD = DC,$

$\Rightarrow$ $\Delta AED = \Delta ABC$ (A đúng).

$\Rightarrow$ $BC = BD$ (hai cạnh tương ứng) (B đúng);

$\widehat {ABC} = \widehat {ABD}$ (hai góc tương ứng) (D đúng).

Câu 5 :

A

$\widehat {CBD} = \widehat {CAD}$
B

$\widehat {CBD} < \widehat {CAD}$
C

$\widehat {CBD} > \widehat {CAD}$
D

$2.\widehat {CBD} = \widehat {CAD}$

Đáp án : A

Phương pháp giải :

+ Sử dụng tính chất hai tam giác bằng nhau ở ý trước suy ra hai góc tương ứng bằng nhau

+ Sau đó sử dụng tính chất hai góc kề bù hoặc góc ngoài để so sánh hai góc $\widehat {CAD}$ và $\widehat {CBD}.$

Lời giải chi tiết :

Xét tam giác $OAD$ và tam giác $OBC$ có

$OA = OB,$

$\widehat O$ chung,

$OC = OD$

$\Rightarrow$ $\Delta OAD = \Delta OBC$ ( c.g.c)

$\Rightarrow$ $\widehat {OBC} = \widehat {OAD}$ (hai góc tương ứng bằng nhau)

Lại có $\widehat {OBC} + \widehat {CBD} = 180^\circ ;\,\widehat {OAD} + \widehat {DAC} = 180^\circ$ (hai góc kề bù)

Nên $\widehat {CBD} = 180^\circ - \widehat {OBC}$ và $\widehat {CAD} = 180^\circ - \widehat {OAD}$ mà $\widehat {OBC} = \widehat {OAD}$ (cmt)

$\Rightarrow$ $\widehat {CBD} = \widehat {CAD}.$

Câu 6 :

Cho tam giác $ABC$ có $AB = AC = BC,$ phân giác $BD$ và $CE$ cắt nhau tại $O.$ Tính $\widehat {BOC}.$

A

${60^0}$
B

${80^0}$
C

$120^\circ$
D

${100^0}$

Đáp án : C

Phương pháp giải :

Sử dụng tính chất tia phân giác, tính chất hai góc kề bù và định lý tổng ba góc trong tam giác.

Lời giải chi tiết :

Vì $BD$ và $CE$ là tia phân giác của góc $\widehat {ABC}$ và $\widehat {ACB}$ nên $\widehat {ABD} = \widehat {CBD}$ và $\widehat {ACE} = \widehat {BCE}.$

Xét tam giác $ABD$ và tam giác $CBD$ có:

+ $AB = AC\,\left( {gt} \right)$

+ $\widehat {ABD} = \widehat {CBD}$ (cmt)

+ Cạnh $BD$ chung

Suy ra $\Delta ABD = \Delta CBD\,\left( {c - g - c} \right)$ $\Rightarrow \widehat {BCA} = \widehat {BAC}$ (hai góc tương ứng) (1)

Tương tự ta có $\Delta BCE = \Delta ACE\left( {c - g - c} \right)$ $\Rightarrow \widehat {CBA} = \widehat {BAC}$ (hai góc tương ứng) (2)

Từ (1) và (2) ta có $\widehat {ABC} = \widehat {BAC} = \widehat {ACB}$ . Mà $\widehat {ABC} + \widehat {BAC} + \widehat {ACB} = 180^\circ$ (định lý tổng ba góc của tam giác) nên $\widehat {ABC} = \widehat {BAC} = \widehat {ACB} = \frac{{180^\circ }}{3} = 60^\circ .$

Lại có $\widehat {ABD} = \widehat {CBD}$ (cmt) nên $\widehat {CBO} = \frac{{\widehat {ABC}}}{2} = \frac{{60^\circ }}{2} = 30^\circ$ ; $\widehat {ACE} = \widehat {BCE} = \frac{{\widehat {ACB}}}{2} = \frac{{60^\circ }}{2} = 30^\circ .$

Xét tam giác $BOC$ có $\widehat {BOC} + \widehat {OBC} + \widehat {OCB} = 180^\circ$ (định lý tổng ba góc của một tam giác)

Nên $\widehat {BOC} = 180^\circ - 30^\circ - 30^\circ = 120^\circ .$

Vậy $\widehat {BOC} = 120^\circ .$

Câu 7 :

A

$4\,cm$
B

$2cm$
C

$3\,cm$
D

$3,5\,cm$

Đáp án : A

Phương pháp giải :

Dùng trường hợp bằng nhau thứ hai để chứng minh hai tam giác bằng nhau, từ đó có các cạnh và các góc tương ứng. Lập luận để có được $O$ là trung điểm của $EF$ để tính độ dài $EF.$

Lời giải chi tiết :

* Xét tam giác $OBC$ và $OAD$ có

+ $OA = OB\,\left( {gt} \right)$

+ $\widehat {AOD} = \widehat {BOC}$ (đối đỉnh)

+ $OC = OD\left( {gt} \right)$

$\Rightarrow$ $\Delta OAD = \Delta OBC\left( {c - g - c} \right)$ nên $\widehat {OAD} = \widehat {OBC}$ (hai góc tương ứng)

* Xét tam giác $OBF$ và $OAE$ có

+ $OA = OB\,\left( {gt} \right)$

+ $\widehat {OAD} = \widehat {OBC}$ (cmt)

+ $BF = AE\left( {gt} \right)$

$\Rightarrow$ $\Delta OBF = \Delta OAE\left( {c - g - c} \right)$

$\Rightarrow$ $OE = OF$ (hai cạnh tương ứng) và $\widehat {AOE} = \widehat {FOB}$ (hai góc tương ứng)

Mà $\widehat {FOB} + \widehat {FOA} = 180^\circ$ (hai góc kề bù) nên $\widehat {FOA} + \widehat {AOE} = 180^\circ$

$\Rightarrow$ 3 điểm $F;\,O;E$ thẳng hàng và $OE = OF$ nên $O$ là trung điểm của $EF \Rightarrow EF = 2.OE = 4\,cm.$

Câu 8 :

Cho tam giác $ABC$ có $AB = AC.$ Trên các cạnh $AB$ và $AC$ lấy các điểm $D,E$ sao cho $AD = AE.$ Gọi $K$ là giao điểm của $BE$ và $CD$ . Chọn câu sai.

A

$BE = CD$
B

$BK = KC$
C

$BD = CE$
D

$DK = KC$

Đáp án : D

Phương pháp giải :

Chứng minh 2 tam giác bằng nhau rồi dựa vào tính chất hai tam giác bằng nhau suy ra các cạnh tương ứng bằng nhau.

Lời giải chi tiết :

Xét tam giác $ABE$ và tam giác $ADC$ có

+ $AD = AE\left( {gt} \right)$

+ Góc $A$ chung

+ $AB = AC\left( {gt} \right)$

$\Rightarrow$ $\Delta ABE = \Delta ACD\left( {c - g - c} \right)$

$\Rightarrow \widehat {ABE} = \widehat {ACD};\widehat {ADC} = \widehat {AEB}$ (hai góc tương ứng) và $BE = CD$ (hai cạnh tương ứng) nên A đúng.

Lại có $\widehat {ADC} + \widehat {BDC} = 180^\circ$ ; $\widehat {AEB} + \widehat {BEC} = 180^\circ$ (hai góc kề bù) mà $\widehat {ADC} = \widehat {AEB}$ (cmt)

$\Rightarrow$ $\widehat {BDC} = \widehat {BEC}.$

Lại có $AB = AC;\,AD = AE\left( {gt} \right)$ $\Rightarrow AB - AD = AC - AE \Rightarrow BD = EC$ nên C đúng.

Xét tam giác $KBD$ và tam giác $KCE$ có

$\widehat {ABE} = \widehat {ACD}\,\left( {cmt} \right)$

$BD = EC\,\left( {cmt} \right)$

$\widehat {BDC} = \widehat {BEC}\,\left( {cmt} \right)$

$\Rightarrow$ $\Delta KBD = \Delta KCE\left( {g - c - g} \right)$

$\Rightarrow KB = KC;\,KD = KE$ (hai cạnh tương ứng) nên B đúng, D sai.

Câu 9 :

Cho tam giác $DEF$ và tam giác $HKG$ có $\widehat D = \widehat H$ , $\widehat E = \widehat K$ , $DE = HK.$ Biết $\widehat F = {80^0}$ . Số đo góc $G$ là:

A

${70^0}$
B

${80^0}$
C

${90^0}$
D

${100^0}$

Đáp án : B

Phương pháp giải :

Áp dụng trường hợp bằng nhau thứ ba của tam giác để chứng minh hai tam giác bằng nhau, từ đó suy ra tính chất về góc của hai tam giác bằng nhau.

Lời giải chi tiết :

Xét tam giác $DEF$ và tam giác $HKG$ có $\widehat D = \widehat H$ , $\widehat E = \widehat K$ , $DE = HK,$ do đó $\Delta DEF = \Delta HKG$ (g.C.g).

Do đó $\widehat G = \widehat F = {80^0}$ (hai góc tương ứng).

Câu 10 :

Cho tam giác $ABC$ vuông tại $A$ có $AB = AC.$ Qua $A$ kẻ đường thẳng $xy$ sao cho $B,C$ nằm cùng phía với $xy.$ Kẻ $BD$ và $CE$ vuông góc với $xy.$ Chọn câu đúng.

A

$DE = BD + CE$
B

$DE = BD - CE$
C

$CE = BD + DE$
D

$CE = BD - DE$

Đáp án : A

Phương pháp giải :

+ Dựa vào hệ quả của trường hợp bằng nhau thứ ba của tam giác để chứng minh các cặp tam giác bằng nhau

+ Từ các cặp cạnh tương ứng bằng nhau ta lập luận để suy ra mối quan hệ đúng.

Lời giải chi tiết :

Ta có: ${\widehat A_1} + {\widehat A_2} = {90^0}\,\,\,\left( {do\,\,\,\widehat {BAC} = {{90}^0}} \right)$

Mà ${\widehat A_1} + {\widehat B_2} = {90^0}$ (vì tam giác $ABD$ vuông tại $D.$ )

$\Rightarrow {\widehat B_2} = {\widehat A_2}$ (cùng phụ với ${\widehat A_1}$ ).

Lại có ${\widehat A_2} + {\widehat C_1} = {90^0}$ (vì tam giác $ACE$ vuông tại $E$ )

$\Rightarrow {\widehat A_1} = {\widehat C_1}$ (cùng phụ với ${\widehat A_2}$ ).

Xét hai tam giác $BDA$ và $AEC$ có:

$\widehat {{B_2}} = \widehat {{A_2}}$ ; $AB = AC$ (gt) và $\widehat {{A_1}} = \widehat {{C_1}}$ (cmt)

$\Rightarrow \Delta BA{\rm{D}} = \Delta ACE$ (g.c.g)

$\Rightarrow$ $BD = AE$ (hai cạnh tương ứng), $CE = AD$ (hai cạnh tương ứng).

Do đó $DE = AD + AE = CE + BD.$

Cho tam giác $ABC$ vuông tại $A.$ Tia phân giác của góc $ABC$ cắt $AC$ tại $D,$ lấy $E$ trên cạnh $BC$ sao cho $BE = AB.$

Câu 11

Chọn câu đúng.

A.

$\Delta ABD{\rm{ }} = \Delta EBD$
B.

$\Delta ABD{\rm{ }} = \Delta BED$
C.

$DC = DE$
D.

$\Delta ABD = \Delta CBD$

Đáp án : A

Phương pháp giải :

Sử dụng trường hợp bằng nhau thứ hai của tam giác để chứng minh $\Delta ABD{\rm{ }} = \Delta EBD$ .

Lời giải chi tiết :

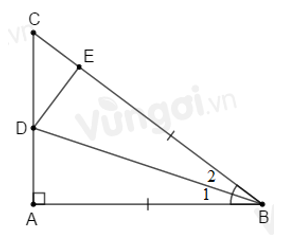Xét $\Delta ABD$ và $\Delta EBD$ có:

$BA = BE$ (gt)

$\widehat {{B_1}} = \widehat {{B_2}}$ (vì $BD$ là tia phân giác $\widehat {ABC}$ )

$BD$ cạnh chung

$\Rightarrow \Delta ABD{\rm{ }} = \Delta EBD\,(c.g.c)$

Câu 12

Trên tia đối của tia $DE$ lấy điểm $M$ sao cho $DM = DC$ . So sánh $EC$ và $AM$ .

A.

$EC < AM$
B.

$EC = AM$
C.

$EC > AM$
D.

Chưa đủ điều kiện để so sánh

Đáp án : B

Phương pháp giải :

- Sử dụng kết quả câu trước $\Delta ABD{\rm{ }} = \Delta EBD$ suy ra $DE = DA$ (hai cạnh tương ứng).

- Sử dụng trường hợp bằng nhau thứ hai của tam giác để chứng minh $\Delta ADM = \Delta EDC$ từ đó suy ra điều phải chứng minh.

Lời giải chi tiết :

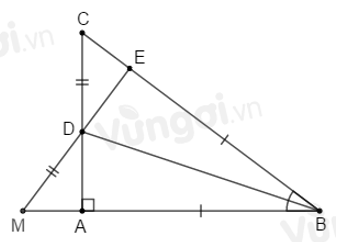Sử dụng kết quả câu trước $\Delta ABD{\rm{ }} = \Delta EBD$ suy ra $DE = DA$ (hai cạnh tương ứng). Nối $AM.$

Xét $\Delta ADM$ và $\Delta EDC$ có:

$DA = DE$ (chứng minh trên)

$\widehat {ADM} = \widehat {EDC}$ (hai góc đối đỉnh)

$DM = DC\,(gt)$

$\Rightarrow \Delta ADM = \Delta EDC\,(c.g.c)$

$\Rightarrow AM = EC$ (hai cạnh tương ứng bằng nhau).

Câu 13

Trên tia đối của tia $DE$ lấy điểm $M$ sao cho $DM = DC$ . Nối $AE,$ so sánh số đo $\widehat {AEC};\widehat {EAM}$ .

A.

$\widehat {AEC} > \widehat {EAM}$
B.

$\widehat {AEC} < \widehat {EAM}$
C.

$\widehat {AEC} = \widehat {EAM}$
D.

Chưa đủ điều kiện so sánh

Đáp án : C

Phương pháp giải :

- Sử dụng kết quả câu trước $\Delta ADM = \Delta EDC$ suy ra $AD = ED;\,AM = EC$ (các cạnh tương ứng).

- Sử dụng trường hợp bằng nhau thứ nhất của tam giác để chứng minh $\Delta AEC = \Delta EAM$ , từ đó suy ra điều phải chứng minh.

Lời giải chi tiết :

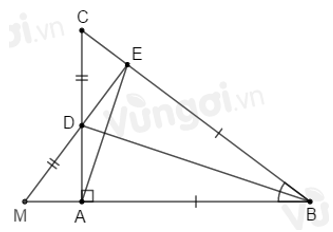Sử dụng kết quả câu trước $\Delta ADM = \Delta EDC$ suy ra $AD = ED;\,AM = EC$ (các cạnh tương ứng).

Ta có: $AD = ED\,\,\,\,(1)$

$DC = DM\,\,\,(2)$

Cộng (1) và (2) theo vế với vế ta được: $AD + DC = ED + DM$ hay $AC = EM$ .

Xét $\Delta AEC$ và $\Delta EAM$ có:

$AE$ cạnh chung

$EC = AM\,(cmt)$

$AC = EM\,(cmt)$

$\Rightarrow \Delta AEC = \Delta EAM\,(c.c.c)$

$\Rightarrow \widehat {AEC} = \widehat {EAM}$ (hai góc tương ứng).

Câu 14

So sánh $OB;OC$ .

A.

$OB < OC$
B.

$OB = OC$
C.

$OB > OC$
D.

$OB \ge OC$

Đáp án : B

Phương pháp giải :

Sử dụng trường hợp bằng nhau thứ hai của tam giác để chứng minh $\Delta OAH = \Delta OBH$ , $\Delta OAK = \Delta OCK$ . Từ đó suy ra các cạnh tương ứng bằng nhau.

Lời giải chi tiết :

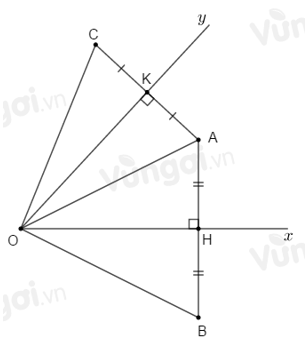Xét $\Delta OAH$ và $\Delta OBH$ có:

$OH$ cạnh chung

$\widehat {OHA} = \widehat {OHB} = {90^o}$

$HA = HB\,(gt)$

$\Rightarrow \Delta OAH = \Delta OBH\,(c.g.c)$

$\Rightarrow OA = OB$ (hai cạnh tương ứng) (1)

Xét $\Delta OAK$ và $\Delta OCK$ có:

$OK$ cạnh chung

$\widehat {OKA} = \widehat {OKC} = {90^o}$

$KA = KC\,(gt)$

$\Rightarrow \Delta OAK = \Delta OCK\,(c.g.c)$

$\Rightarrow OA = OC$ (hai cạnh tương ứng) (2)

Từ (1) và (2) suy ra $OA = OB = OC.$

Câu 15

Biết $\widehat {xOy} = \alpha .$ Tính $\widehat {BOC}.$

A.

$3\alpha$
B.

$4\alpha$
C.

$2\alpha$
D.

$\alpha$

Đáp án : C

Phương pháp giải :

Sử dụng kết quả câu trước ta có: $\Delta OAH = \Delta OBH$ , $\Delta OAK = \Delta OCK$ . Từ đó suy ra $\widehat {BOH} = \widehat {AOH}$ , $\widehat {AOK} = \widehat {COK}$ (các cặp góc tương ứng), sau đó biến đổi để tìm được số đo của $\widehat {BOC}.$

Lời giải chi tiết :

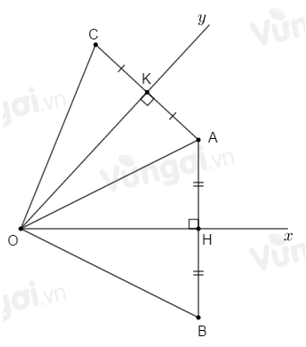Sử dụng kết quả câu trước ta có: $\Delta OAH = \Delta OBH$ , $\Delta OAK = \Delta OCK$ .

Vì $\Delta OAH = \Delta OBH$ suy ra $\widehat {BOH} = \widehat {AOH}$ (hai góc tương ứng).

Vì $\Delta OAK = \Delta OCK$ suy ra $\widehat {AOK} = \widehat {COK}$ (hai góc tương ứng).

Ta có $\widehat {BOC} = \widehat {BOA} + \widehat {AOC}$

$\Rightarrow \widehat {BOC} = \widehat {BOH} + \widehat {AOH} + \widehat {AOK} + \widehat {COK}$

$\Rightarrow \widehat {BOC} = 2\widehat {AOH} + 2\widehat {AOK}$ (vì $\widehat {BOH} = \widehat {AOH}$ và $\widehat {AOK} = \widehat {COK}$ )

$\Rightarrow \widehat {BOC} = 2\left( {\widehat {AOH} + \widehat {AOK}} \right) = 2\widehat {xOy} = 2\alpha .$

Câu 16 :

A

$4\,cm$
B

$2cm$
C

$3\,cm$
D

$3,5\,cm$

Đáp án : A

Phương pháp giải :

Lời giải chi tiết :

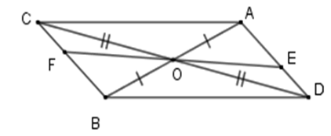* Xét tam giác $OBC$ và $OAD$ có

+ $OA = OB\,\left( {gt} \right)$

+ $\widehat {AOD} = \widehat {BOC}$ (đối đỉnh)

+ $OC = OD\left( {gt} \right)$

Suy ra $\Delta OAD = \Delta OBC\left( {c - g - c} \right)$ nên $\widehat {OAD} = \widehat {OBC}$ (hai góc tương ứng)

* Xét tam giác $OBF$ và $OAE$ có

+ $OA = OB\,\left( {gt} \right)$

+ $\widehat {OAD} = \widehat {OBC}$ (cmt)

+ $BF = AE\left( {gt} \right)$

Suy ra $\Delta OBF = \Delta OAE\left( {c - g - c} \right)$ nên $OE = OF$ (hai cạnh tương ứng) và $\widehat {AOE} = \widehat {FOB}$ (hai góc tương ứng)

Mà $\widehat {FOB} + \widehat {FOA} = 180^\circ$ (hai góc kề bù) nên $\widehat {FOA} + \widehat {AOE} = 180^\circ$

Suy ra ba điểm $F;\,O;E$ thẳng hàng và $OE = OF$ nên $O$ là trung điểm của $EF \Rightarrow EF = 2.OE = 4\,cm.$

Câu 17 :

(I) $\Delta AMD = \Delta BMC$

(II) $\Delta ANE = \Delta CNB$

(III) $A,D,E$ thẳng hàng

(IV) $A$ là trung điểm của đoạn thẳng $DE$

Số khẳng định đúng trong các khẳng định trên là

A

$0$
B

$2$
C

$4$
D

$3$

Đáp án : C

Phương pháp giải :

(I), (II) Dựa vào trường hợp bằng nhau thứ hai của tam giác để chứng minh các tam giác bằng nhau

(III) Để chứng minh ba điểm $A,D,E$ thẳng hàng ta chứng minh $A$ có hai đường thẳng $AD,AE$ cùng song song với $BC.$

(IV) Để chứng minh $A$ là trung điểm của $DE$ ta chứng minh $AD$ và $AE$ cùng bằng $BC$ do đó chúng bằng nhau.

Lời giải chi tiết :

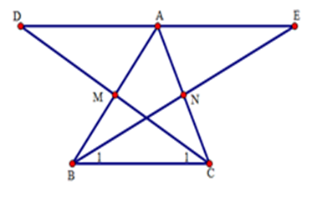(I) Xét $\Delta AMD$ và $\Delta BMC$ có: $DM = MC\left( {gt} \right);$ $\widehat {BMC} = \widehat {AMD}$ (hai góc đối đỉnh); $AM = BM\left( {gt} \right),$ nên $\Delta AMD = \Delta BMC$ (c.g.c).

(II) Xét $\Delta ANE$ và $\Delta CNB$ có: $AN = NC\left( {gt} \right);$ $\widehat {ANE} = \widehat {CNB}$ (hai góc đối đỉnh), $NB = NE\left( {gt} \right),$ do đó

$\Delta CNB = \Delta ANE$ (c.g.c).

(III) Do $\Delta AMD = \Delta BMC$ nên $\widehat D = \widehat {{C_1}}$ (hai góc tương ứng).

Mà hai góc này ở vị trí so le trong nên $AD//BC.$

Do $\Delta CNB = \Delta ANE$ nên $\widehat E = \widehat {{B_1}}$ (hai góc tương ứng).

Mà hai góc này ở vị trí so le trong nên $AE//BC.$

Như vậy qua $A$ có hai đường thẳng $AD,AE$ cùng song song với $BC.$

Do đó $D,A,E$ thẳng hàng. (1)

(IV) Ta có: $AD = BC$ (do $\Delta AMD = \Delta BMC$ ); $AE = BC$ (do $\Delta CNB = \Delta ANE$ ) nên $AD = AE\left( 2 \right)$

Từ (1) và (2) suy ra $A$ là trung điểm của $DE.$

Vậy cả (I); (II); (III); (IV) đều đúng.

Câu 18

Chọn câu sai.

A.

$AC = OB$
B.

$AC = BC$
C.

$\widehat {OAC} = \widehat {OBC}$
D.

$CO$ là tia phân giác của $\widehat {BCA}.$

Đáp án : A

Phương pháp giải :

Chứng minh hai tam giác bằng nhau theo trường hợp thứ hai và tính chất hai tam giác bằng nhau.

Lời giải chi tiết :

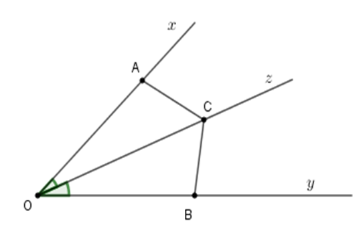Xét tam giác $AOC$ và $BOC$ có

+ $OA = OB\left( {gt} \right)$

+ $\widehat {AOC} = \widehat {BOC}$ (tính chất tia phân giác)

+ Cạnh $OC$ chung

Suy ra $\Delta AOC = \Delta BOC\left( {c - g - c} \right)$

$\Rightarrow AC = BC$ (hai cạnh tương ứng); $\widehat {OAC} = \widehat {OBC}$ ; $\widehat {OCA} = \widehat {OCB}$ (hai góc tương ứng)

Từ đó $CO$ là tia phân giác của $\widehat {BCA}.$

Nên B, C, D đúng, A sai.

Câu 19

Gọi $I$ là giao của $AB$ và $Oz.$ Tính góc $AIC.$

A.

$120^\circ$
B.

$90^\circ$
C.

$60^\circ$
D.

${100^0}$

Đáp án : B

Phương pháp giải :

Sử dụng trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh

Lời giải chi tiết :

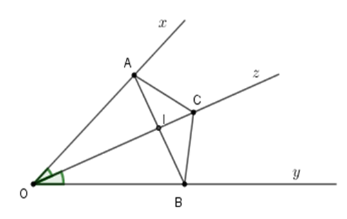Xét tam giác $AOI$ và $BOI$ có

+ $OA = OB\left( {gt} \right)$

+ $\widehat {AOI} = \widehat {BOI}$ (tính chất tia phân giác)

+ Cạnh $OI$ chung

Suy ra $\Delta AOI = \Delta BOI\left( {c - g - c} \right)$

Do đó $\widehat {AIO} = \widehat {BIO}$ (hai góc tương ứng) mà $\widehat {AIO} + \widehat {BIO} = 180^\circ$ nên $\widehat {AIO} = \widehat {BIO} = \dfrac{{180^\circ }}{2} = 90^\circ$

Hay $OC \bot AB \Rightarrow \widehat {AIC} = 90^\circ .$

Cho tam giác $ABC$ có $AB = AC = BC,$ phân giác $BD$ và $CE$ cắt nhau tại $O.$

Câu 20

Chọn câu đúng.

A.

$CE \bot \;AB$
B.

$BD\; \bot AC$
C.

$DC = BC$
D.

Cả A, B đều đúng.

Đáp án : D

Phương pháp giải :

Dựa vào tính chất hai tam giác bằng nhau và tính chất hai góc kề bù.

Lời giải chi tiết :

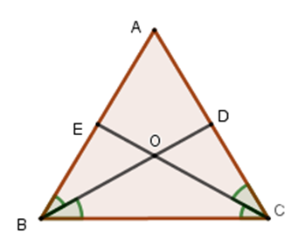Vì $BD$ và $CE$ là tia phân giác của góc $\widehat {ABC}$ và $\widehat {ACB}$ nên $\widehat {ABD} = \widehat {CBD}$ và $\widehat {ACE} = \widehat {BCE}.$

Xét tam giác $ABD$ và tam giác $CBD$ có:

+ $AB = AC\,\left( {gt} \right)$

+ $\widehat {ABD} = \widehat {CBD}$ (cmt)

+ Cạnh $BD$ chung

Suy ra $\Delta ABD = \Delta CBD\,\left( {c - g - c} \right)$

$\Rightarrow \widehat {ADB} = \widehat {BDC}$ (hai góc tương ứng); $DC = AD$ (hai cạnh tương ứng) nên C sai.

Mà $\widehat {ADB} + \widehat {CDB} = 180^\circ$ (hai góc kề bù)

Nên $\widehat {ADB} = \widehat {CDB} = \dfrac{{180^\circ }}{2} = 90^\circ$ . Do đó $BD \bot AC.$

Tương tự ta có $CE \bot AB.$

Câu 21

Tính $\widehat {BOC}.$

A.

${60^0}$
B.

${80^0}$
C.

$120^\circ$
D.

${100^0}$

Đáp án : C

Phương pháp giải :

Sử dụng tính chất tia phân giác, tính chất hai góc kề bù và định lý tổng ba góc trong tam giác.

Lời giải chi tiết :

Từ câu trước ta có $\Delta ABD = \Delta CBD\,\left( {c - g - c} \right)$ $\Rightarrow \widehat {BCA} = \widehat {BAC}$ (hai góc tương ứng) (1)

Tương tự ta có $\Delta BCE = \Delta ACE\left( {c - g - c} \right)$ $\Rightarrow \widehat {CBA} = \widehat {BAC}$ (hai góc tương ứng) (2)

Lại có $\widehat {ABD} = \widehat {CBD}$ (cmt) nên $\widehat {CBO} = \dfrac{{\widehat {ABC}}}{2} = \dfrac{{60^\circ }}{2} = 30^\circ$ ; $\widehat {ACE} = \widehat {BCE} = \dfrac{{\widehat {ACB}}}{2} = \dfrac{{60^\circ }}{2} = 30^\circ .$

Xét tam giác $BOC$ có $\widehat {BOC} + \widehat {OBC} + \widehat {OCB} = 180^\circ$ (định lý tổng ba góc của một tam giác)

Nên $\widehat {BOC} = 180^\circ - 30^\circ - 30^\circ = 120^\circ .$

Vậy $\widehat {BOC} = 120^\circ .$

Câu 22 :

Cho đoạn thẳng $AB$ , trên đường trung trực $d$ của đoạn $AB$ lấy điểm $M.$ So sánh $AM$ và $BM.$

A

$MA = MB$
B

$MA > MB$
C

$MA < MB$
D

$2.MA = MB$

Đáp án : A

Phương pháp giải :

Sử dụng hai tam giác bằng nhau theo trường hợp cạnh-cạnh-cạnh từ đó suy ra $AM = BM.$

Lời giải chi tiết :

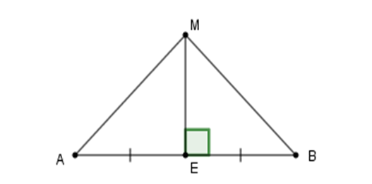Đường trung trực của $AB$ vuông góc với $AB$ tại trung điểm $E$ . Do đó $ME \bot AB;\,EA = EB.$

Xét tam giác $MEA$ và tam giác $MEB$ có $EA = EB\,\left( {cmt} \right),$ $\widehat {MEA} = \widehat {MEB} = 90^\circ ,$ cạnh $ME$ chung nên $\Delta MEA = \Delta MEB\,\left( {c - g - c} \right)$ suy ra $MA = MB$ (hai cạnh tương ứng).

Câu 23 :

Cho tam giác $ABC$ có $\widehat A = {90^0}$ , tia phân giác $BD$ của góc $B$ ( $D \in AC$ ). Trên cạnh $BC$ lấy điểm $E$ sao cho $BE = BA.$ Hai góc nào sau đây bằng nhau?

A

$\widehat {EDC};\widehat {BAC}$
B

$\widehat {EDC};\widehat {ACB}$
C

$\widehat {EDC};\widehat {ABC}$
D

$\widehat {EDC};\widehat {EC{\rm{D}}}$

Đáp án : C

Phương pháp giải :

Sử dụng trường hợp bằng nhau thứ hai của tam giác để suy ra $\widehat {BED} = \widehat {BAD} = 90^\circ$ và lập luận để chỉ ra $\widehat {EDC} = \widehat {ABC}.$

Lời giải chi tiết :

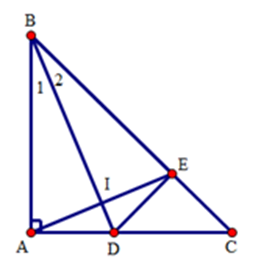Xét hai tam giác $BDA$ và $BDE$ có: $BA = BE\left( {gt} \right),$ $\widehat {{B_1}} = \widehat {{B_2}}$ (do $BD$ là tia phân giác của góc B);

$BD$ là cạnh chung. Suy ra $\Delta BDA = \Delta BDE$ (c.g.c)

Suy ra $\widehat {BED} = \widehat {BAD} = {90^ \circ }$ (hai góc tương ứng)

Trong các tam giác $ABC$ và $EDC$ vuông ở $A$ và $E,$ ta có:

$\widehat {ABC} + \widehat C = {90^ \circ }$ và $\widehat {EDC} + \widehat C = {90^ \circ }$ , suy ra $\widehat {EDC} = \widehat {ABC}$ .

Câu 24 :

Cho tam giác $DEF$ và tam giác $HKG$ có $DE = HK$ , $\widehat E = \widehat K$ , $EF = KG.$ Biết $\widehat D = {70^0}$ . Số đo góc $H$ là:

A

${70^0}$
B

${80^0}$
C

${90^0}$
D

${100^0}$

Đáp án : A

Phương pháp giải :

+Sử dụng trường hợp bằng nhau thứ hai của tam giác để chứng minh hai tam giác bằng nhau từ đó suy ra hai góc tương ứng bằng nhau.

Lời giải chi tiết :

Xét tam giác $DEF$ và tam giác $HKG$ có $DE = HK$ , $\widehat E = \widehat K$ , $EF = KG.$

do đó $\Delta DEF = \Delta HKG$ (c.g.c).

Do đó $\widehat H = \widehat D = {70^0}$ (hai góc tương ứng).

Cho góc nhọn $xOy.$ Trên tia $Ox$ lấy hai điểm $A,C,$ trên tia $Oy$ lấy hai điểm $B,D$ sao cho $OA = OB,OC = OD$ ( $A$ nằm giữa $O$ và $C,$ $B$ nằm giữa $O$ và $D$ ).

Câu 25

Chọn câu đúng.

A.

$\Delta OAD = \Delta OCB$
B.

$\Delta ODA = \Delta OBC$
C.

$\Delta AOD = \Delta BCO$
D.

$\Delta OAD = \Delta OBC$ .

Đáp án : D

Lời giải chi tiết :

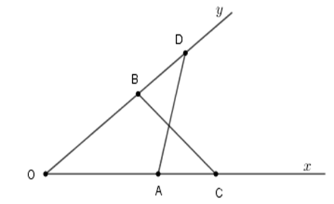Xét tam giác $OAD$ và tam giác $OBC$ có

$OA = OB,$ góc $O$ chung, $OD = OC$ suy ra $\Delta OAD = \Delta OBC\,\left( {c - g - c} \right).$

Câu 26

So sánh hai góc $\widehat {CAD}$ và $\widehat {CBD}.$

A.

$\widehat {CBD} = \widehat {CAD}$
B.

$\widehat {CBD} < \widehat {CAD}$
C.

$\widehat {CBD} > \widehat {CAD}$
D.

$\widehat {CBD} =2.\widehat {CAD}$ .

Đáp án : A

Phương pháp giải :

Sử dụng tính chất hai tam giác bằng nhau ở ý trước suy ra hai góc tương ứng bằng nhau

Sau đó sử dụng tính chất hai góc kề bù hoặc góc ngoài để so sánh hai góc $\widehat {CAD}$ và $\widehat {CBD}.$

Lời giải chi tiết :

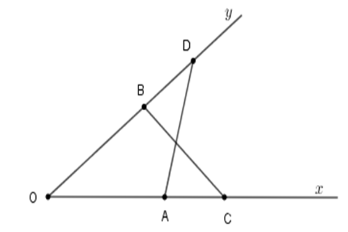Vì $\Delta OAD = \Delta OBC\,\left( {c - g - c} \right).$ Suy ra $\widehat {OBC} = \widehat {OAD}$ (hai góc tương ứng bằng nhau)

Lại có $\widehat {OBC} + \widehat {CBD} = 180^\circ ;\,\widehat {OAD} + \widehat {DAC} = 180^\circ$ (hai góc kề bù)

Nên $\widehat {CBD} = 180^\circ - \widehat {OBC}$ và $\widehat {CAD} = 180^\circ - \widehat {OAD}$ mà $\widehat {OBC} = \widehat {OAD}$ (cmt)

Suy ra $\widehat {CBD} = \widehat {CAD}.$

Câu 27 :

Cho tam giác $BAC$ và tam giác $KEF$ có $BA = EK,$ $\widehat A = \widehat K$ , $CA = KF.$ Phát biểu nào trong trong các phát biểu sau đây là đúng:

A

$\Delta BAC = \Delta EKF$
B

$\Delta BAC = \Delta EFK$
C

$\Delta {\rm A}BC = \Delta FKE$
D

$\Delta BAC = \Delta KEF$

Đáp án : A

Lời giải chi tiết :

Xét tam giác $BAC$ và tam giác $KEF$ có $BA = EK,$ $\widehat A = \widehat K$ , $CA = KF.$ Suy ra $\Delta BAC = \Delta EKF$ (c.g.c)

Câu 28 :

A

$BC = MK$
B

$BC = HK$
C

$AC = MK$
D

$AC = HK$

Đáp án : C

Lời giải chi tiết :

Để tam giác $ABC$ và tam giác $MHK$ bằng nhau theo trường hợp cạnh – góc – cạnh cần thêm điều kiện về cạnh kề đó là: $AC = MK.$

Chú ý

Hai tam giác bằng nhau theo trường hợp cạnh - góc -cạnh thì góc phải là góc xen giữa hai cạnh.

Câu 29 :

A

$\widehat M = \widehat A$
B

$\widehat A = \widehat P$
C

$\widehat C = \widehat M$
D

$\widehat A = \widehat N$

Đáp án : C

Lời giải chi tiết :

Áp dụng trường hợp bằng nhau thứ ba của tam giác ta thấy cần thêm điều kiện về góc kề cạnh đó là $\widehat C = \widehat M.$

Câu 30 :

Cho tam giác $ABC$ và tam giác $MNP$ có $\widehat B = \widehat N = {90^ \circ }$ , $AC = MP,$ $\widehat C = \widehat M$ . Phát biểu nào trong các phát biểu sau đây là đúng:

A

$\Delta ABC = \Delta PMN$
B

$\Delta ACB = \Delta PNM$
C

$\Delta BAC = \Delta MNP$
D

$\Delta ABC = \Delta PNM$

Đáp án : D

Phương pháp giải :

Sử dụng hệ quả của trường hợp bằng nhau thứ ba của tam giác: Nếu cạnh huyền và góc nhọn của tam giác này bằng cạnh huyền và góc nhọn của tam giác kia thì hai tam giác đó bằng nhau.

Lời giải chi tiết :

Xét tam giác $ABC$ và tam giác $MNP$ có $\widehat B = \widehat N = {90^ \circ }$ , $AC = MP$ , $\widehat C = \widehat M$ , do đó $\Delta ABC = \Delta PNM$ (cạnh huyền – góc nhọn)

Câu 31 :

Cho tam giác $DEF$ và tam giác $HKG$ có $\widehat D = \widehat H$ , $\widehat E = \widehat K$ , $DE = HK.$ Biết $\widehat F = {80^0}$ . Số đo góc $G$ là:

A

${70^0}$
B

${80^0}$
C

${90^0}$
D

${100^0}$

Đáp án : B

Phương pháp giải :

+Áp dụng trường hợp bằng nhau thứ ba của tam giác để chứng minh hai tam giác bằng nhau, từ đó suy ra tính chất về góc của hai tam giác bằng nhau.

Lời giải chi tiết :

Xét tam giác $DEF$ và tam giác $HKG$ có $\widehat D = \widehat H$ , $\widehat E = \widehat K$ , $DE = HK,$ do đó $\Delta DEF = \Delta HKG$ (g.c.g).

Do đó $\widehat G = \widehat F = {80^0}$ (hai góc tương ứng).

Câu 32 :

Cho tam giác $ABC$ và tam giác $DEF$ có $AB = DE,$ $\widehat B = \widehat E$ , $\widehat A = \widehat D$ . Biết $AC = 6cm.$ Độ dài $DF$ là:

A

$4cm\;\;\;\;$
B

$5cm$
C

$6cm\;\;\;\;$
D

$7cm$

Đáp án : C

Phương pháp giải :

+ Áp dụng trường hợp bằng nhau thứ ba của tam giác để chứng minh hai tam giác bằng nhau, từ đó suy ra tính chất về cạnh của hai tam giác bằng nhau.

Lời giải chi tiết :

Xét tam giác $ABC$ và tam giác $DEF$ có $AB = DE,$ $\widehat B = \widehat E$ , $\widehat A = \widehat D$ , do đó $\Delta ABC = \Delta DEF\,\left( {g - c - g} \right)$ .

Do đó $DF = AC = 6cm$ (hai cạnh tương ứng).

Câu 33 :

Cho tam giác $ABC$ vuông tại $A$ có $AB = AC.$ Qua $A$ kẻ đường thẳng $xy$ sao cho $B,C$ nằm cùng phía với $xy.$ Kẻ $BD$ và $CE$ vuông góc với $xy.$ Chọn câu đúng.

A

$DE = BD + CE$
B

$DE = BD - CE$
C

$CE = BD + DE$
D

$CE = BD - DE$

Đáp án : A

Phương pháp giải :

+ Dựa vào hệ quả của trường hợp bằng nhau thứ ba của tam giác để chứng minh các cặp tam giác bằng nhau

+ Từ các cặp cạnh tương ứng bằng nhau ta lập luận để suy ra mối quan hệ đúng.

Lời giải chi tiết :

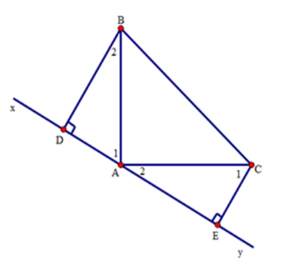Ta có: ${\widehat A_1} + {\widehat A_2} = {90^0}\,\,\,\left( {do\,\,\,\widehat {BAC} = {{90}^0}} \right)$

Mà ${\widehat A_1} + {\widehat B_2} = {90^0}$ vì tam giác $ABD$ vuông tại $D.$

$\Rightarrow {\widehat B_2} = {\widehat A_2}$ (cùng phụ với ${\widehat A_1}$ ).

Lại có ${\widehat A_2} + {\widehat C_1} = {90^0}$ vì tam giác $ACE$ vuông tại $E$

$\Rightarrow {\widehat A_1} = {\widehat C_1}$ (cùng phụ với ${\widehat A_2}$ ).

Xét hai tam giác vuông $BDA$ và $AEC$ có:

$\widehat D = \widehat E = {90^0}$ ; $AB = AC$ (gt) và $\widehat {{A_1}} = \widehat {{C_1}}$ (cmt)

$\Rightarrow \Delta BA{\rm{D}} = \Delta ACE$ (cạnh huyền – góc nhọn)

Suy ra $BD = AE$ (hai cạnh tương ứng), $CE = AD$ (hai cạnh tương ứng).

Do đó $DE = AD + AE = CE + BD.$

Câu 34 :

A

$\Delta ADE = \Delta EFC$
B

$\Delta ADE = \Delta DBF$
C

$\Delta EFC = \Delta DBF$
D

Cả A, B, C đều đúng.

Đáp án : D

Phương pháp giải :

+ Từ tính chất của hai đường song song suy ra các cặp góc bằng nhau, từ đó dựa vào trường hợp bằng nhau thứ ba của tam giác để chứng minh các tam giác bằng nhau

+ Từ các cặp cạnh bằng nhau ta tìm mối liên hệ giữa chúng để suy ra điều phải chứng minh

Lời giải chi tiết :

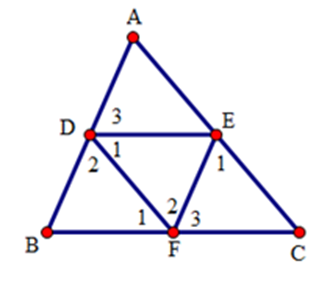Xét tam giác $DEF$ và tam giác $FBD$ có:

$\widehat {{D_1}} = \widehat {{F_1}}$ (hai góc so le trong).

$DF$ là cạnh chung

$\widehat {{F_2}} = \widehat {{D_2}}$ (hai góc so le trong).

Vậy $\Delta DEF = \Delta FBD\,\,\,(g.c.g)$

Suy ra $EF = BD$ (hai cạnh tương ứng)

Mà $AD = BD$ nên $EF = AD$

Ta có : $\widehat {{F_3}} = \widehat B$ (hai góc đồng vị); $\widehat {{D_3}} = \widehat B$ (hai góc đồng vị)

$\Rightarrow \widehat {{D_3}} = \widehat {{F_3}}\left( { = \widehat B} \right).$ .

Xét tam giác $ADE$ và tam giác $EFC$ có:

$\widehat {{D_3}} = \widehat {{F_3}}$ (cmt)

$\widehat A = \widehat {{E_1}}$ (hai góc đồng vị)

$AD = EF\left( {cmt} \right)$

$\Rightarrow \Delta ADE = \Delta EFC\,\,\,(g.c.g).$ (1)

Tương tự ta chứng minh được $\Delta EFC = \Delta DBF\,\,\,(g.c.g)$ (2)

Từ (1) và (2) suy ra $\Delta ADE = \Delta EFC = \Delta DBF$ (3)

Câu 35 :

A

$ID = 4cm$
B

$ID = 2cm$
C

$ID = 8cm$
D

$ID = 3cm$

Đáp án : B

Phương pháp giải :

+ Kẻ tia phân giác của $\widehat {BIC}$ cắt $BC$ tại $H$

+ Sử dụng tính chất tia phân giác, định lí tổng ba góc của một tam giác chứng minh $\widehat {CID} = \widehat {BIE} = \widehat {BIH} = \widehat {HIC} = 60^\circ$ .

+ Áp dụng trường hợp bằng nhau thứ ba của tam giác: “Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau” ta chứng minh $\Delta BIE = \Delta BIH$ , $\Delta CID = \Delta CIH$ .

+ Từ đó ta tính được độ dài $ID$ .

Lời giải chi tiết :

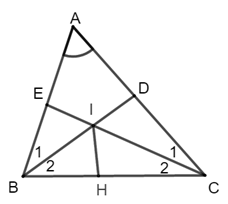Vì $BD$ là tia phân giác của $\widehat {ABC}$ nên $\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{1}{2}\widehat {ABC}$

Vì $CE$ là tia phân giác của $\widehat {ACB}$ nên $\widehat {{C_1}} = \widehat {{C_2}} = \dfrac{1}{2}\widehat {ACB}$

Xét $\Delta ABC$ có: $\widehat A + \widehat {ABC} + \widehat {ACB} = 180^\circ$ (tổng ba góc của một tam giác bằng $180^\circ$ )

Mà $\widehat A = 60^\circ$ nên $\widehat {ABC} + \widehat {ACB} = 180^\circ - \widehat A = 180^\circ - 60^\circ = 120^\circ$

Ta lại có: $\widehat {{B_2}} + \widehat {{C_2}} = \dfrac{1}{2}\widehat {ABC} + \dfrac{1}{2}\widehat {ACB} = \dfrac{1}{2}(\widehat {ABC} + \widehat {ACB}) = \dfrac{1}{2}.120^\circ = 60^\circ$

Xét $\Delta BIC$ có $\widehat {BIC} + \widehat {{B_2}} + \widehat {{C_2}} = 180^\circ$ (tổng ba góc của một tam giác bằng $180^\circ$ )

Mà $\widehat {{B_2}} + \widehat {{C_2}} = 60^\circ$ nên $\widehat {BIC} = 180^\circ - (\widehat {{B_2}} + \widehat {{C_2}}) = 180^\circ - 60^\circ = 120^\circ$

Mặt khác: $\widehat {BIC} + \widehat {BIE} = 180^\circ$ (hai góc kề bù) $\Rightarrow \widehat {BIE} = 180^\circ - \widehat {BIC} = 180^\circ - 120^\circ = 60^\circ$

Khi đó $\widehat {CID} = \widehat {BIE} = 60^\circ$ (hai góc đối đỉnh) $(1)$

Kẻ tia phân giác của $\widehat {BIC}$ cắt $BC$ tại $H$

Suy ra $\widehat {BIH} = \widehat {HIC} = \dfrac{1}{2}.\widehat {BIC} = \dfrac{1}{2}.120^\circ = 60^\circ$ $(2)$

Từ $(1)$ và $(2)$ suy ra $\widehat {CID} = \widehat {BIE} = \widehat {BIH} = \widehat {HIC}$

Xét tam giác $BIE$ và tam giác $BIH$ có:

$\widehat {{B_1}} = \widehat {{B_2}}$ (cmt)

$BI$ là cạnh chung

$\widehat {BIE} = \widehat {BIH}$ (cmt)

$\Rightarrow \Delta BIE = \Delta BIH \,(g.c.g) \Rightarrow IE = IH$ (hai cạnh tương ứng) $(3)$

Xét tam giác $CID$ và tam giác $CIH$ có:

$\widehat {{C_1}} = \widehat {{C_2}}$ (cmt)

$CI$ là cạnh chung

$\widehat {CID} = \widehat {HIC}$ (cmt)

$\Rightarrow \Delta CID = \Delta CIH \,(g.c.g) \Rightarrow ID = IH$ (hai cạnh tương ứng) $(4)$

Từ $(3)$ và $(4)$ suy ra $ID = IE = 2cm$

Câu 36 :

Cho hai đoạn thẳng $AB,CD$ song song với nhau. Hai đoạn thẳng này chắn giữa hai đường thẳng song song $AC,BD$ . Chọn câu đúng:

A

$AB = CD$
B

$AB > CD$
C

$AB < CD$
D

$AC > BD$

Đáp án : A

Phương pháp giải :

+ Kẻ đoạn thẳng $AD$ .

+ Từ tính chất của hai đường thẳng song song suy ra các cặp góc bằng nhau.

+ Áp dụng trường hợp bằng nhau thứ ba của tam giác: “Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau” để chứng minh $\Delta ABD = \Delta DCA$ . Từ đó suy ra các cạnh tương ứng bằng nhau.

Lời giải chi tiết :

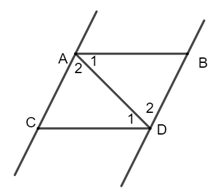Kẻ đoạn thẳng $AD$

Vì $AB//CD$ (gt) nên $\widehat {{A_1}} = \widehat {{D_1}}$ (hai góc so le trong)

Vì $AC//BD$ (gt) nên $\widehat {{A_2}} = \widehat {{D_2}}$ (hai góc so le trong)

Xét tam giác $ABD$ và tam giác $DCA$ có:

$\widehat {{A_1}} = \widehat {{D_1}}$ (cmt)

$AD$ là cạnh chung

$\widehat {{A_2}} = \widehat {{D_2}}$ (cmt)

$\Rightarrow \Delta ABD = \Delta DCA\,(g.c.g) \Rightarrow AB = CD$ (hai cạnh tương ứng); $AC = BD$ (hai cạnh tương ứng)

Bài liên quan

Trắc nghiệm Bài 15: Các trường hợp bằng nhau của tam giác vuông Toán 7 Kết nối tri thức

Luyện tập và củng cố kiến thức Bài 15: Các trường hợp bằng nhau của tam giác vuông Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Trắc nghiệm Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng Toán 7 Kết nối tri thức với cuộc sống

Luyện tập và củng cố kiến thức Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Trắc nghiệm Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác Toán 7 Kết nối tri thức

Luyện tập và củng cố kiến thức Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Trắc nghiệm Bài 12: Tổng các góc trong một tam giác Toán 7 Kết nối tri thức

Luyện tập và củng cố kiến thức Bài 12: Tổng các góc trong một tam giác Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Trắc nghiệm Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác Toán 7 Kết nối tri thức

Trắc nghiệm Bài 15: Các trường hợp bằng nhau của tam giác vuông Toán 7 Kết nối tri thức

Trắc nghiệm Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng Toán 7 Kết nối tri thức với cuộc sống

Trắc nghiệm Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác Toán 7 Kết nối tri thức

Trắc nghiệm Bài 12: Tổng các góc trong một tam giác Toán 7 Kết nối tri thức